题目内容
用数学归纳法证明
+cosα+cos3α+…+cos（2n-1）α=
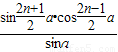（k∈Z*，α≠kπ，n∈N+），在验证n=1时，左边计算所得的项是 ．
【答案】分析：由等式
+cosα+cos3α+…+cos（2n-1）α=
，当n=1时，2n-1=1，而等式左边起始为
的，后面再加上α的连续的正整数倍的余弦值的和，由此易得答案．
解答：解：在等式
+cosα+cos3α+…+cos（2n-1）α=
中，
当n=1时，2n-1=1，
而等式左边起始为
的，后面再加上α的连续的正整数倍的余弦值的和，
故n=1时，等式左边的项为：
+cosα，
故答案为：
+cosα．
点评：本题考查的知识点是数学归纳法的步骤，在数学归纳法中，第一步是论证n=1时结论是否成立，此时一定要分析等式两边的项，不能多写也不能少写，否则会引起答案的错误．解此类问题时，注意n的取值范围．
+cosα+cos3α+…+cos（2n-1）α=，当n=1时，2n-1=1，而等式左边起始为的，后面再加上α的连续的正整数倍的余弦值的和，由此易得答案．解答：解：在等式
+cosα+cos3α+…+cos（2n-1）α=中，当n=1时，2n-1=1，
而等式左边起始为
的，后面再加上α的连续的正整数倍的余弦值的和，故n=1时，等式左边的项为：
+cosα，故答案为：
+cosα．点评：本题考查的知识点是数学归纳法的步骤，在数学归纳法中，第一步是论证n=1时结论是否成立，此时一定要分析等式两边的项，不能多写也不能少写，否则会引起答案的错误．解此类问题时，注意n的取值范围．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
在用数学归纳法证明（n+1）（n+2）…（n+n）=2n•1•2•3•…•（2n-1）（n∈N*）时，从k到k+1，左端需要增加的代数式是（ ）
| A、2k+1 | ||
| B、2（2k+1） | ||
C、
| ||
D、
|
用数学归纳法证明不等式“
+
+…+
＞
（n＞2）”时的过程中，由n=k到n=k+1时，不等式的左边（ ）
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2n |
| 13 |
| 24 |
A、增加了一项
| ||||||
B、增加了两项
| ||||||
C、增加了两项
| ||||||
D、增加了一项
|