题目内容
设变量x,y满足约束条件
,且目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,则a+b= .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:先画出满足约束条件
的可行域,平移目标函数,找出目标函数z1=2x+3y的最大值为a,目标函数z2=3x-2y的最小值为b,即可.
|
解答:
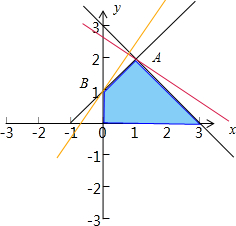 解:由约束条件
解:由约束条件
得如图所示的阴影区域,
由目标函数z1=2x+3y可得:y=-
x+
z1,
显然当平行直线过点A,即
的交点A(1,2)时,
z1取得最大值为8;
由目标函数z2=3x-2y可得:y=
x-
z2,
显然当平行直线过点B(0,1)时,
z2取得最小值为-2;
a+b=6,
故答案为:6.
 解:由约束条件
解:由约束条件
|
由目标函数z1=2x+3y可得:y=-
| 2 |
| 3 |
| 1 |
| 3 |
显然当平行直线过点A,即
|
z1取得最大值为8;
由目标函数z2=3x-2y可得:y=
| 3 |
| 2 |
| 1 |
| 2 |
显然当平行直线过点B(0,1)时,
z2取得最小值为-2;
a+b=6,
故答案为:6.
点评:在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.

练习册系列答案
相关题目
已知命题p:存在x0∈R,x02-x0+1<0;命题q:“x>0,a=1”是“x+
≥2”的充分不必要条件”.则下列命题正确的是( )
| a |
| x |
| A、命题“p或q”是假命题 |
| B、命题“(¬p)且q”是真命题 |
| C、命题“p或(¬q)”是真命题 |
| D、命题“(¬p)且(¬q)”是真命题 |
已知
,则x2+y2的最小值是( )
|
| A、3 | ||
B、
| ||
C、
| ||
D、
|
在△ABC中,内角A,B,C所对的边长分别是a,b,c.若c-acosB=(2a-b)cosA,则△ABC的形状为( )
| A、等腰三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等腰或直角三角形 |
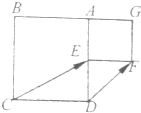 如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则
如图,已知正方形ABCD的边长为2,点E为边AD的中点,以AE为边向外作正方形AEFG,现将正方形AEFG绕点A按顺时针方向转动至AE与AB重合,则