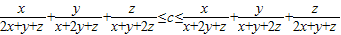题目内容
(附加题)是否存在常数c,使得不等式
+
+
≤c≤
+
+
对于任意正数x,y,z恒成立?试证明你的结论.
| x |
| 2x+y+z |
| y |
| x+2y+z |
| z |
| x+y+2z |
| x |
| x+2y+z |
| y |
| x+y+2z |
| z |
| 2x+y+z |
对于任意正数x,y,z恒成立?试证明你的结论.
分析:利用x=y=z时,猜测常数c,左边不等式利用换元法,再利用基本不等式可证;右边不等式的证明,用柯西不等式、分析法证明即可.
解答:解:猜测常数c=
(可以猜测等号当且仅当x=y=z时成立)
左边不等式的证明方法,令
,则
,
∴左边=
+
+
=
-(
+
)-(
+
)-(
+
)≤
右边不等式的证明用柯西不等式证明,证法如下:
右边=
+
+
=
+
+
=
≥
,
于是要证明右边不等式成立,只需证明
≥
,
即证4(x+y+z)2≥3[x2+y2+z2+3(xy+yz+xz)}
即证:x2+y2+z2≥xy+yz+xz
即证:(x-y)2+(y-z)2+(x-z)2≥0
显然成立,故问题得证.
| 3 |
| 4 |
左边不等式的证明方法,令
|
|
∴左边=
| 3a-b-m |
| 4a |
| 3b-a-m |
| 4b |
| 3m-a-b |
| 4m |
| 9 |
| 4 |
| b |
| 4a |
| a |
| 4b |
| m |
| 4a |
| a |
| 4m |
| b |
| 4m |
| m |
| 4b |
| 3 |
| 4 |
右边不等式的证明用柯西不等式证明,证法如下:
右边=
| x |
| x+2y+z |
| y |
| x+y+2z |
| z |
| 2x+y+z |
| x2 |
| x2+2xy+xz |
| y2 |
| yx+y2+2yz |
| z2 |
| 2xz+yz+z2 |
=
(
| ||||||
| ((x2+2xy+xz)+(yx+y2+2yz)+(2xz+yz+z2)) |
| (x+y+z)2 |
| x2+y2+z2+3(xy+yz+xz) |
于是要证明右边不等式成立,只需证明
| (x+y+z)2 |
| x2+y2+z2+3(xy+yz+xz) |
| 3 |
| 4 |
即证4(x+y+z)2≥3[x2+y2+z2+3(xy+yz+xz)}
即证:x2+y2+z2≥xy+yz+xz
即证:(x-y)2+(y-z)2+(x-z)2≥0
显然成立,故问题得证.
点评:本题的考点是分析法与综合法,考查利用分析法证明不等式,考查基本不等式的运用,注意分析法的证题步骤是解题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目