题目内容
14.已知数列{an}的前n项和为Sn,且满足a1=2,Sn-4Sn-1-2=0(n≥2,n∈Z).(Ⅰ)求数列{an}的通项公式;
(Ⅱ)令bn=log2an,Tn为{bn}的前n项和,求证$\sum_{i=1}^{n}$$\frac{1}{{T}_{k}}$<2.
分析 (I)利用数列递推关系、等比数列的通项公式即可得出.
(II)利用“裂项求和”方法、数列的单调性即可得出.
解答 解:(Ⅰ)当n≥3时,可得Sn-4Sn-1-2-(Sn-1-4Sn-2-2)=0(n≥2,n∈Z).∴an=4an-1,
又因为a1=2,代入表达式可得a2=8,满足上式.
所以数列{an}是首项为a1=2,公比为4的等比数列,故:an=2×4n-1=22n-1.
(Ⅱ)证明:bn=log2an=2n-1.
Tn=$\frac{n(1+2n-1)}{2}$=n2.
n≥2时,$\frac{1}{{T}_{n}}$=$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}-\frac{1}{n}$.
$\sum_{i=1}^{n}$$\frac{1}{{T}_{k}}$≤1+$(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n-1}-\frac{1}{n})$=2-$\frac{1}{n}$<2.
点评 本题考查了数列递推关系、等比数列的通项公式、“裂项求和”方法、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
5.“微信抢红包”自2015年以来异常火爆,在某个微信群某次进行的抢红包活动中,若所发红包的总金额为10元,被随机分配为1.49元,1.81元,2.19元,3.41元,0.62元,0.48元,共6份,供甲、乙等6人抢,每人只能抢一次,则甲、乙二人抢到的金额之和不低于4元的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
9.设集合A={x|x2-4x+3<0},B={x|log2x>1},则A∩B=( )
| A. | (-1,3) | B. | (-1,2) | C. | (1,3) | D. | (2,3) |
6.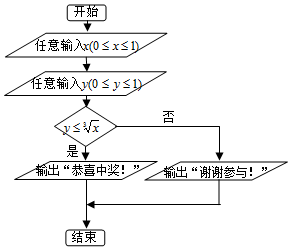 在如图的程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图的程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
 在如图的程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )
在如图的程序框图中,任意输入一次x(0≤x≤1)与y(0≤y≤1),则能输出“恭喜中奖!”的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
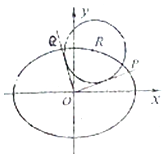 如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于P,Q两点.
如图,在平面直角坐标系xOy中,已知R(x0,y0)是椭圆C:$\frac{x^2}{24}+\frac{y^2}{12}$=1上的一点,从原点O向圆R:(x-x0)2+(y-y0)2=8作两条切线,分别交椭圆于P,Q两点.