题目内容
19.已知f(x)=ex-ax2,g(x)是f(x)的导函数.(Ⅰ)求g(x)的极值;
(Ⅱ)若f(x)≥x+(1-x)•ex在x≥0时恒成立,求实数a的取值范围.
分析 (Ⅰ)g(x)=f'(x)=ex-2ax,g'(x)=ex-2a,分a≤0,a>0讨论;
(Ⅱ)f(x)≥x+(1-x)ex,即ex-ax2≥x+ex-xex,即ex-ax-1≥0,
令h(x)=ex-ax-1,分a≤1,a>1讨论求得实数a的取值范围;
解答 解:(Ⅰ)f(x)=ex-ax2,g(x)=f'(x)=ex-2ax,g'(x)=ex-2a,
当a≤0时,g'(x)>0恒成立,g(x)无极值;
当a>0时,g'(x)=0,即x=ln(2a),
由g'(x)>0,得x>ln(2a);由g'(x)<0,得x<ln(2a),
所以当x=ln(2a)时,有极小值2a-2aln(2a).
(Ⅱ)f(x)≥x+(1-x)ex,即ex-ax2≥x+ex-xex,即ex-ax-1≥0,
令h(x)=ex-ax-1,则h'(x)=ex-a,
当a≤1时,由x≥0知h'(x)≥0,∴h(x)≥h(0)=0,原不等式成立,
当a>1时,h'(x)=0,即x=lna,h'(x)>0,得x>lna;h'(x)<0,得x<lna,
所以h(x)在(0,lna)上单调递减,
又∵h(0)=0,∴a>1不合题意,
综上,a的取值范围为(-∞,1].
点评 本题考查了导数的综合应用,分类讨论思想、转化思想,属于中档题.

练习册系列答案
相关题目
10.“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
(1)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的2×2列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附:${k^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,
(2)若小王以这40位好友该日走路步数的频率分布来估计其所有微信好友每日走路步数的概率分布,现从小王的所有微信好友中任选2人,其中每日走路不超过5000步的有X人,超过10000步的有Y人,设ξ=|X-Y|,求ξ的分布列及数学期望.
| 步数 性别 | 0~2000 | 2001~5000 | 5001~8000 | 8001~10000 | >10000 |
| 男 | 1 | 2 | 3 | 6 | 8 |
| 女 | 0 | 2 | 10 | 6 | 2 |
| 积极型 | 懈怠型 | 总计 | |
| 男 | 14 | 8 | 22 |
| 女 | 6 | 12 | 18 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
7. 共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
(Ⅰ)已知该校大一学生由2400人,求抽取的100名学生中大一学生人数;
(Ⅱ)作出这些数据的频率分布直方图;
(Ⅲ)估计该校大学生每周使用共享单车的平均时间$\overline t$(同一组中的数据用该组区间的中点值作代表).
 共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:
共享单车的出现方便了人们的出行,深受我市居民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生中按年级用分层抽样的方式随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)如表:| 使用时间 | [0,2] | (2,4] | (4,6] | (6,8] | (8,10] |
| 人数 | 10 | 40 | 25 | 20 | 5 |
(Ⅱ)作出这些数据的频率分布直方图;
(Ⅲ)估计该校大学生每周使用共享单车的平均时间$\overline t$(同一组中的数据用该组区间的中点值作代表).
14.设(1+i)(x+yi)=2,其中i为虚数单位,x,y是实数,则|2x+yi|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
8.已知$\overrightarrow{a}$为单位向量,$\overrightarrow{b}$=(0,2),且$\overrightarrow{a}$$•\overrightarrow{b}$=1,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
9.已知函数f(x)=x2+bx+c在x=-1处取得极值-1,那么f(x)=( )
| A. | x2-2x-4 | B. | x2+x-1 | C. | x2+2x | D. | x2-2 |
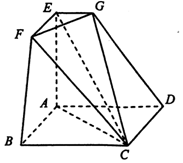 如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.
如图所示的空间几何体ABCDEFG中,四边形ABCD是边长为2的正方形,AE⊥平面ABCD,EF∥AB,EG∥AD,EF=EG=1.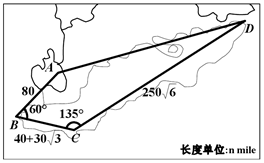 某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.
某沿海四个城市A、B、C、D的位置如图所示,其中∠ABC=60°,∠BCD=135°,AB=80nmile,BC=40+30$\sqrt{3}$nmile,CD=250$\sqrt{6}$nmile,D位于A的北偏东75°方向.现在有一艘轮船从A出发以50nmile/h的速度向D直线航行,60min后,轮船由于天气原因收到指令改向城市C直线航行,收到指令时城市C对于轮船的方位角是南偏西θ度,则sinθ=$\frac{{\sqrt{6}-\sqrt{2}}}{4}$.