题目内容
已知函数
(Ⅰ)当 时,求
时,求 的极值;
的极值;
(Ⅱ)若 在区间
在区间 上是增函数,求实数
上是增函数,求实数 的取值范围.
的取值范围.
【答案】
(Ⅰ)极小值为1+ln2,函数无极大值;(Ⅱ) .
.
【解析】
试题分析:(Ⅰ)首先确定函数的定义域(此步容易忽视),把 代入函数,再进行求导,列
代入函数,再进行求导,列 的变化情况表,即可求函数的极值;(Ⅱ)先对函数求导,得
的变化情况表,即可求函数的极值;(Ⅱ)先对函数求导,得 ,再对
,再对 分
分 和
和 两种情况讨论(此处易忽视
两种情况讨论(此处易忽视 这种情况),由题意函数
这种情况),由题意函数 在区间
在区间 是增函数,则
是增函数,则 对
对 恒成立,即不等式
恒成立,即不等式 对
对 恒成立,从而再列出
恒成立,从而再列出 应满足的关系式,解出
应满足的关系式,解出 的取值范围.
的取值范围.
试题解析:(Ⅰ)函数的定义域为 , 1分
, 1分
 ,当a=0时,
,当a=0时, ,则
,则 , 3分
, 3分
∴ 的变化情况如下表
的变化情况如下表
|
x |
(0, |
|
( |
|
|
- |
0 |
+ |
|
|
|
极小值 |
|
∴当 时,
时,
 的极小值为1+ln2,函数无极大值.
7分
的极小值为1+ln2,函数无极大值.
7分
(Ⅱ)由已知,得
 , 8分
, 8分
若 ,由
,由 得
得 ,显然不合题意,
9分
,显然不合题意,
9分
若 ∵函数
∵函数 区间
区间 是增函数,
是增函数,
∴ 对
对 恒成立,即不等式
恒成立,即不等式 对
对 恒成立,
恒成立,
即  恒成立, 11分
恒成立, 11分
故 ,而当
,而当 ,函数
,函数 , 13分
, 13分
∴实数 的取值范围为
的取值范围为 .
14分
.
14分
另解: ∵函数 区间
区间 是增函数
是增函数 ,
,
 对
对 恒成立,即不等式
恒成立,即不等式 对
对 恒成立,
恒成立,
设 ,
, 恒成立
恒成立 恒成立,
恒成立,
若 ,由
,由 得
得 ,显然不符合题意;
,显然不符合题意;
若 ,由
,由 ,
, 无解,显然不符合题意;
无解,显然不符合题意;
若 ,
,  ,故
,故 ,解得
,解得 ,所以实数
,所以实数 的取值范围为
的取值范围为 .
.
考点:1、函数的极值;2、导函数的性质及综合应用.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 )
)


 .
. 时,求
时,求 的单调区间;
的单调区间; 单调增加,在
单调增加,在 单调减少,证明:
单调减少,证明: <6.
<6.
 时,求
时,求 的解集
的解集 的不等式
的不等式 的解集是
的解集是 ,求
,求 的取值范围
的取值范围 .
. 时,求
时,求 的极小值;
的极小值; 对任意的
对任意的 都不是曲线
都不是曲线 的切线,求
的切线,求 的取值范围.
的取值范围.

 时,求曲线
时,求曲线 在点
在点 处的切线方程;
处的切线方程;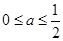 时,讨论
时,讨论 的单调性
的单调性