题目内容
已知函数f(x)满足2f(x)-f(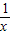 )=
)=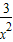 ,则f(x)的最小值是( )
,则f(x)的最小值是( )A.2
B.2
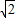
C.3
D.4
【答案】分析:令x=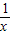 ,原式可变为2f(
,原式可变为2f(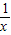 )-f(x)=3x2,与已知联立可得f(x)解析式,用基本不等式即可求得f(x)的最小值.
)-f(x)=3x2,与已知联立可得f(x)解析式,用基本不等式即可求得f(x)的最小值.
解答:解:由2f(x)-f(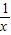 )=
)=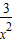 ①,得2f(
①,得2f(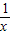 )-f(x)=3x2②,
)-f(x)=3x2②,
联立①②解得f(x)=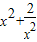 ,
,
f(x)=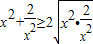 =2
=2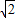 ,当且仅当
,当且仅当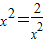 ,即x=
,即x=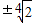 时取等号,
时取等号,
故f(x)的最小值为2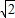 .
.
点评:本题考查了函数解析式的求解方法及函数最值问题,解决本题关键是令x=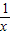 构造另一等式,注意基本不等式求最值的条件.
构造另一等式,注意基本不等式求最值的条件.
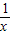 ,原式可变为2f(
,原式可变为2f(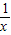 )-f(x)=3x2,与已知联立可得f(x)解析式,用基本不等式即可求得f(x)的最小值.
)-f(x)=3x2,与已知联立可得f(x)解析式,用基本不等式即可求得f(x)的最小值.解答:解:由2f(x)-f(
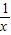 )=
)=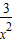 ①,得2f(
①,得2f(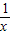 )-f(x)=3x2②,
)-f(x)=3x2②,联立①②解得f(x)=
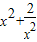 ,
,f(x)=
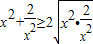 =2
=2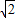 ,当且仅当
,当且仅当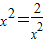 ,即x=
,即x=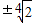 时取等号,
时取等号,故f(x)的最小值为2
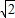 .
.点评:本题考查了函数解析式的求解方法及函数最值问题,解决本题关键是令x=
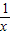 构造另一等式,注意基本不等式求最值的条件.
构造另一等式,注意基本不等式求最值的条件. 
练习册系列答案
相关题目