题目内容
已知函数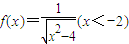 ,点
,点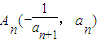 在曲线y=f(x)的图象上(n∈N*),且a1=1.
在曲线y=f(x)的图象上(n∈N*),且a1=1.(1)证明数列{
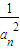 }为等差数列;
}为等差数列;(2)求数列{an}的通项公式
(3)设bn=
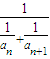 ,记Sn=b1+b2+…+bn,求Sn.
,记Sn=b1+b2+…+bn,求Sn.
【答案】分析:(1)把点An代入函数f(x)中化简整理 判断出数列{
判断出数列{ }为等差数列.
}为等差数列.
(2)先根据数列{ }为等差数列,并且首项为
}为等差数列,并且首项为 =1,公差为4,求得
=1,公差为4,求得 ,进而求得数列{an}的通项公式
,进而求得数列{an}的通项公式
(3)把(2)中求得an代入bn中,进而用叠加法求得数列的前n项的和.
解答:解:(1)∵点 在曲线y=f(x)的图象上(n∈N*)
在曲线y=f(x)的图象上(n∈N*)
∴
∴
∴ ,∴
,∴ ,
,
∴数列{ }为等差数列.
}为等差数列.
(2)∵数列{ }为等差数列,并且首项为
}为等差数列,并且首项为 =1,公差为4,
=1,公差为4,
∴ =1+4(n-1),∴
=1+4(n-1),∴ ,
,
∵an>0,∴ ,
,
(3)bn= =
= ,
,
∴Sn=b1+b2++bn
= =
=
点评:本题主要考查了数列等差关系的确定和通项公式.解题的基础是对数列公式的熟练掌握.
 判断出数列{
判断出数列{ }为等差数列.
}为等差数列.(2)先根据数列{
 }为等差数列,并且首项为
}为等差数列,并且首项为 =1,公差为4,求得
=1,公差为4,求得 ,进而求得数列{an}的通项公式
,进而求得数列{an}的通项公式(3)把(2)中求得an代入bn中,进而用叠加法求得数列的前n项的和.
解答:解:(1)∵点
 在曲线y=f(x)的图象上(n∈N*)
在曲线y=f(x)的图象上(n∈N*)∴

∴

∴
 ,∴
,∴ ,
,∴数列{
 }为等差数列.
}为等差数列.(2)∵数列{
 }为等差数列,并且首项为
}为等差数列,并且首项为 =1,公差为4,
=1,公差为4,∴
 =1+4(n-1),∴
=1+4(n-1),∴ ,
,∵an>0,∴
 ,
,(3)bn=
 =
= ,
,∴Sn=b1+b2++bn
=
 =
=
点评:本题主要考查了数列等差关系的确定和通项公式.解题的基础是对数列公式的熟练掌握.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
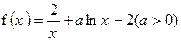
 y=x+2垂直,求函数y=f(x)的单调区间;[来源:学&科&网Z&X&X&K]
y=x+2垂直,求函数y=f(x)的单调区间;[来源:学&科&网Z&X&X&K] 成立,试求a的取值范围;
成立,试求a的取值范围;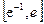 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。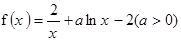
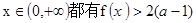 成立,试求a的取值范围;
成立,试求a的取值范围;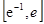 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。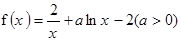
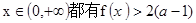 成立,试求a的取值范围;
成立,试求a的取值范围;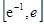 上有两个零点,求实数b的取值范围。
上有两个零点,求实数b的取值范围。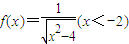 ,点
,点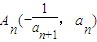 在曲线y=f(x)的图象上(n∈N*),且a1=1.
在曲线y=f(x)的图象上(n∈N*),且a1=1.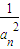 }为等差数列;
}为等差数列;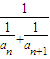 ,记Sn=b1+b2+…+bn,求Sn.
,记Sn=b1+b2+…+bn,求Sn.