题目内容
解下列关于x方程(1)2x2+4x+1=0
(2)x2+2x+a+1=0(a∈R)
【答案】分析:(1)由于判别式△=42-4×2×1=8,利用求根公式求得方程的两个实数根.
(2)先求出判别式△的值,当△≥0时,用求根公式求得方程的根,当△<0时,方程无解.
解答:解:(1)由于判别式△=42-4×2×1=8,利用求根公式求得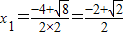 ,(3分)
,(3分)
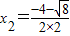 =
=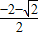 . (3分)
. (3分)
解:(2)判别式△=4-4(a+1)=-4a,(1分)
当△≥0时,即-4a≥0时,(2分)即a≤0时,(3分)
用求根公式求得方程的根为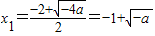 ,
,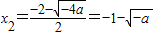 .(5分)
.(5分)
(2)△<0时,-4a<0,即a>0时,方程无解. (6分)
点评:本题主要考查一元二次方程的解法,体现了分类讨论的数学思想,属于基础题.
(2)先求出判别式△的值,当△≥0时,用求根公式求得方程的根,当△<0时,方程无解.
解答:解:(1)由于判别式△=42-4×2×1=8,利用求根公式求得
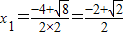 ,(3分)
,(3分)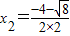 =
=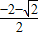 . (3分)
. (3分)解:(2)判别式△=4-4(a+1)=-4a,(1分)
当△≥0时,即-4a≥0时,(2分)即a≤0时,(3分)
用求根公式求得方程的根为
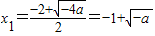 ,
,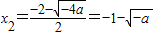 .(5分)
.(5分)(2)△<0时,-4a<0,即a>0时,方程无解. (6分)
点评:本题主要考查一元二次方程的解法,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
