Question

在△ABC中，边a上的高为h，且a=3h，则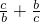的最大值是________．

Answer 1

分析：由于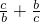=，S_△ABC=ah=bcsinA，于是bc=，结合余弦定理c²+b²=a²+2bccosA，可得到=3sinA+2cosA．利用辅助角公式，问题得到解决．
解答：∵S_△ABC=ah=bcsinA，
∴bc=，又a=3h，
∴由余弦定理c²+b²=a²+2bccosA，
又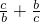===+2cosA=+2cosA
=3sinA+2cosA
=sin（A+θ）（tanθ=）．
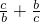∴的最大值是．
故答案为：．
点评：本题考查三角函数的最值，难点在于三角形的面积公式与余弦定理的综合运用，辅助角公式的使用，属于难题．