Question

若曲线y=x²+mx+2与以A(0,1)、B(2,3)为端点的线段AB有两个不同的交点,求实数m的取值范围.(如图所示)

Answer 1

思路解析：有不同的交点即方程组有两组不同的解,也可以数形结合求解.

解法一:∵k_AB=1,

∴线段AB的方程为y=x+1(0≤x≤2).

由方程组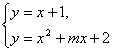消去y并整理,得x²+(m-1)x+1=0.

由Δ=(m-1)²-4＞0,得m＜-1或m＞3.                                             ①

令f(x)=x²+mx+2,显然抛物线恒过点(0,2),即恒有f(0)＞1.于是只需考虑f(2)≥3,即4+2m+2≥3.

∴m≥-.                                                                                ②

∵抛物线的对称轴为x=-,∴0＜-＜2,即-4＜m＜0.                  ③

由①②③式求交集,得m的取值范围是-≤m＜-1.

解法二:∵A(0,1)、B(2,3),

∴线段AB的方程为y=x+1(0≤x≤2).

由方程组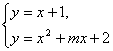消去y并整理,得x²+(m-1)x+1=0.       ①

令f(x)=x²+(m-1)x+1,                                                              ②

则抛物线与线段AB有两个交点的充要条件为方程①在［0,2］上有两个不相等的实数根,即抛物线②在［0,2］上与x轴有两个交点.于是得

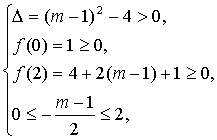解之,得-≤m＜-1.

∴m的取值范围是-≤m＜-1.