题目内容
【题目】已知抛物线
的焦点为
，准线为
，过点的直线交拋物线于
，
两点，过点作准线的垂线，垂足为
，当点坐标为
时，
为正三角形，则此时
的面积为____________
【答案】
【解析】
过F作AE的垂线，垂足为H，则H为AE的中点，利用A点坐标为 （3，y0），可求p，可得抛物线的方程，求出直线AF的方程，与抛物线方程联立求出A，B的坐标，即可求出△OAB的面积．
如图所示，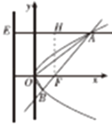
过F作AE的垂线，垂足为H，则H为AE的中点，
因为A点坐标为 （3，y0），
所以AE=3+
，EH=p，
所以2p=3+，
所以p=2，
所以y2=4x，此时A（3，2
），kAF=，
所以直线AF的方程为y=（x﹣1），
代入抛物线方程可得3（x﹣1）2=4x，解得x=3或
，
所以y=2或﹣
，
所以△AOB的面积为
,
故答案为：.
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
