题目内容
9.设函数f(x)为R上的增函数,a、b∈R.求证:a+b≥0的充要条件是f(a)+f(b)≥f(-a)+f(-b).分析 由题意可得a≥-b,b≥-a,由函数的单调性可得不等式,相加可得.
解答 证明:a+b≥0等价于a≥-b,b≥-a,
由函数f(x)为R上的增函数可得f(a)≥f(-a),f(b)≥f(-b),
由不等式的可加性可得f(a)+f(b)≥f(-a)+f(-b).
反之,若f(a)+f(b)≥f(-a)+f(-b),
可设a+b<0,等价于a<-b,b<-a,
由函数f(x)为R上的增函数可得f(a)<f(-b),f(b)<f(-a),
由不等式的可加性可得f(a)+f(b)<f(-a)+f(-b).
这与假设矛盾.则a+b≥0.
∴a+b≥0的充要条件是f(a)+f(b)≥f(-a)+f(-b).
点评 本题考查函数的单调性,涉及充要条件和不等式的性质,属基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.已知8>7,16>9,32>11,…,则有( )
| A. | 2n>2n+1 | B. | 2n+1>2n+1 | C. | 2n+2>2n+5 | D. | 2n+3>2n+7 |
17.在以O为中心,F1,F2为焦点的双曲线上存在一点M,满足|$\overrightarrow{M{F}_{1}}$|=2|$\overrightarrow{MO}$|=2|$\overrightarrow{M{F}_{2}}$|,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
3.已知双曲线E的左,右顶点为A,B,点C在E上,AB=BC,且∠BCA=30°,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
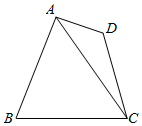 如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.
如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.