题目内容
在直角坐标系中,已知A(-1,0),B(1,0),点M满足
=
,则直线AM的斜率的取值范围为
| MA |
| MB |
| 2 |
[-1,1]
[-1,1]
.分析:设M(x,y),根据
=
由两点间的距离公式化简得x2+y2-6x+1=0.设AM的斜率为k=
,可得y=k(x+1),代入前面的方程化简整理,得到关于x的一元二次方程.最后根据方程有实根利用根的判别式建立关于k的不等式,解之即可得到直线AM的斜率k的取值范围.
| MA |
| MB |
| 2 |
| y |
| x+1 |
解答:解:设M(x,y),直线AM的斜率为k,可得
∵A(-1,0),B(1,0),∴MA=
,MB=
.
∵点M满足
=
,∴MA=
MB,即
=
,
两边平方,得(x+1)2+y2=2[(x-1)2+y2],
化简整理得x2+y2-6x+1=0,
∵AM的斜率为k=
,
∴y=k(x+1),代入上式并化简得(1+k2)x2+(2k2-6)x+k2+1=0.
以上一元二次方程有实数解,可得△=(2k2-6)2-4(1+k2)2≥0,解之得-1≤k≤1.
即直线AM的斜率的取值范围为[-1,1].
故答案为:[-1,1]
∵A(-1,0),B(1,0),∴MA=
| (x+1)2+y2 |
| (x-1)2+y2 |
∵点M满足
| MA |
| MB |
| 2 |
| 2 |
| (x+1)2+y2 |
| 2 |
| (x-1)2+y2 |
两边平方,得(x+1)2+y2=2[(x-1)2+y2],
化简整理得x2+y2-6x+1=0,
∵AM的斜率为k=
| y |
| x+1 |
∴y=k(x+1),代入上式并化简得(1+k2)x2+(2k2-6)x+k2+1=0.
以上一元二次方程有实数解,可得△=(2k2-6)2-4(1+k2)2≥0,解之得-1≤k≤1.
即直线AM的斜率的取值范围为[-1,1].
故答案为:[-1,1]
点评:本题给出点M满足的条件,求M的轨迹并讨论直线斜率的取值范围,着重考查了两点间的距离公式、直线的斜率公式和一元二次方程根与系数的关系等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
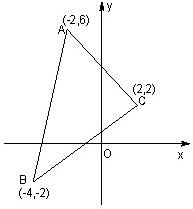 如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求:
如图,在直角坐标系中,已知△ABC的三个顶点的坐标,求: 如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB:
如图,在直角坐标系中,已知射线OA:x-y=0(x≥0),OB: