题目内容

设△ABC中，cosA=
3
5
，sinB=
5
13
，则cosC的值为（　　）
A．
56
65
B．-
16
65
C．
16
65
D．
56
65
或-
16
65
由于△ABC中，cosA=
3
5
，sinB=
5
13
＜
1
2
，∴sinA=
4
5
＞
2
2
，故A＞
π
4
，B＜
π
6
 或B＞
5π
6
（舍去）．
∴cosB=
12
13
，故有cosC=-cos（A+B）=-cosAcosB+sinAsinB=-
3
5
×
12
13
+
4
5
×
5
13
=-
16
65
，
故选B．
练习册系列答案
相关题目
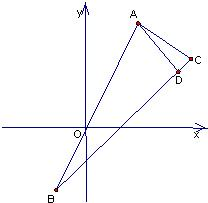精英家教网已知在△ABC中，A（2，4），B（-1，-2），C（4，3），BC边上的高为AD，垂足为D：
（1）求证：AB⊥AC；
（2）求点D和向量
AD
的坐标；
（3）设∠ABC=θ，求cosθ的值；
（4）求证：AD2=BD•DC．
设△ABC中，角A、B、C的对边分别为a、b、c，A、B∈(0，
π
2
)，若b=a•cos（A+B）．
（1）求证：tanB=
tanA
2tan2A+1
；
（2）当tanB取最大值时，求cotC的值．
（2013•河东区一模）已知函数f（x）=sinx+cos（x-
π
6
），x∈R．
（1）求f（x）的最大值；
（2）设△ABC中，角A、B的对边分别为a、b，若B=2A，且b=2af（A-
π
6
），求角C的大小．
已知函数f（x）=sinx+cos（x-
π
6
），x∈R．
（I）求f（x）的单调增区间及f（x）图象的对称轴方程；
（II）设△ABC中，角A、B的对边分别为a、b，若B=2A，且b=2af（A-
π
6
），求角C的大小．
已知△ABC中，A（2，4），B（-1，-2），C（4，3），BC边上的高为AD．

（1）求点D和向量的坐标；

（2）设∠ABC=θ，求cosθ的值；（3）求证：2=｜｜·｜｜．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网