题目内容
设△ABC中,角A、B、C的对边分别为a、b、c,A、B∈(0,| π |
| 2 |
(1)求证:tanB=
| tanA |
| 2tan2A+1 |
(2)当tanB取最大值时,求cotC的值.
分析:(1)根据正弦定理
=
,利用两角和的余弦函数公式及诱导公式化简b=a•cos(A+B)得到即可;
(2)把tanB变形,利用基本不等式求出最大值时tanA的值,然后利用两角和的正切公式求出tan(A+B),利用诱导公式得到tanC即可得到cotC.
| a |
| sinA |
| b |
| sinB |
(2)把tanB变形,利用基本不等式求出最大值时tanA的值,然后利用两角和的正切公式求出tan(A+B),利用诱导公式得到tanC即可得到cotC.
解答:解:(1)由正弦定理,sinB=sinA•(cosAcosB-sinAsinB)=sinA•cosA•cosB-sin2AsinB?(1+sin2A)sinB=sinA•cosAcosB?tanB=
=
=
(2)tanB=
≤
(∵A∈(0,
))
当且仅当2tanA=
即tanA=
时,tanB的最大值
此时,tan(A+B)=
=
=
∵tan(A+B)=-tanC?tanC=-
∴cotC=-
.
| sinA•cosA |
| 1+sin2A |
| sinAcosA |
| 2sin2A+cos2A |
| tanA |
| 2tan2A+1 |
(2)tanB=
| 1 | ||
2tanA+
|
| 1 | ||
2
|
| π |
| 2 |
当且仅当2tanA=
| 1 |
| tanA |
| ||
| 2 |
| ||
| 4 |
此时,tan(A+B)=
| tanA+tanB |
| 1-tanAtanB |
| ||||||||
1-
|
| 2 |
∵tan(A+B)=-tanC?tanC=-
| 2 |
∴cotC=-
| ||
| 2 |
点评:考查学生灵活运用正弦定理解决数学问题,灵活运用两角和与差的正切、余弦函数公式,会进行三角恒等式的证明.

练习册系列答案
相关题目

 ,
,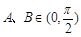 ,若
,若 .
. ;
; 取最大值时,求
取最大值时,求 的值.
的值.