题目内容
(12分)已知 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点 到两焦点的距离分别为4和2,过
到两焦点的距离分别为4和2,过 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点 到两焦点的距离分别为4和2,过
到两焦点的距离分别为4和2,过 点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程.
点作焦点所在轴的垂线,它恰好过椭圆的一个焦点,求椭圆方程. 或
或 .
.本试题主要是考查了椭圆的定义和椭圆的性质,以及焦点三角形中边的比例关系可知得到a,b,c的关系式,从而得到结论。
解:设两焦点为 、
、 ,且
,且 ,
, .
.
从椭圆定义知 .即
.即 .
.
从 知
知 垂直焦点所在的对称轴,
垂直焦点所在的对称轴,
所以在 中,
中, ,
,
可求出 ,
, ,从而
,从而 .
.
∴所求椭圆方程为 或
或 .
.
解:设两焦点为
 、
、 ,且
,且 ,
, .
.从椭圆定义知
 .即
.即 .
.从
 知
知 垂直焦点所在的对称轴,
垂直焦点所在的对称轴,所以在
 中,
中, ,
,可求出
 ,
, ,从而
,从而 .
.∴所求椭圆方程为
 或
或 .
.
练习册系列答案
相关题目
 过点
过点 ,且离心率为
,且离心率为 .
. 的方程;
的方程; 为椭圆
为椭圆 的左、右顶点,直线
的左、右顶点,直线 与
与 轴交于点
轴交于点 ,点
,点 是椭圆
是椭圆 分别交直线
分别交直线 于
于 两点.证明:
两点.证明: 恒为定值.
恒为定值.
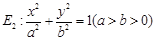 .
.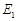 与
与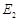 有相同的离心率,过点
有相同的离心率,过点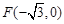 的直线
的直线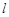 与
与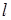 过
过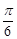 .
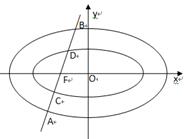
.
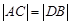 ;
; 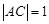 ,求直线
,求直线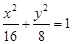 两焦点
两焦点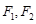 ,则椭圆上存在六个不同点
,则椭圆上存在六个不同点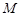 ,使得△
,使得△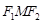 为直角三角形;
为直角三角形;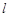 过抛物线
过抛物线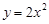 的焦点,且与这条抛物线交于
的焦点,且与这条抛物线交于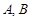 两点,则
两点,则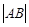 的最小值为2;
的最小值为2;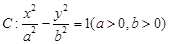 的一个焦点作它的一条渐近线的垂线,垂足为
的一个焦点作它的一条渐近线的垂线,垂足为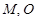 为坐标原点,则
为坐标原点,则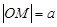 ;
; ,如果
,如果 的最小值为m,则满足
的最小值为m,则满足 的整点
的整点 的个数为 ( )
的个数为 ( ) 的离心率为
的离心率为 ,且过点Q(1,
,且过点Q(1,
 (O为坐标原点),求实数t的最小值.
(O为坐标原点),求实数t的最小值.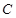 :
: 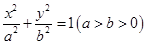 过点(0,4),离心率为
过点(0,4),离心率为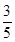 .
.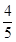 的直线被
的直线被 ,且经过点
,且经过点 ,过椭圆的左焦点作直线
,过椭圆的左焦点作直线 交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。
交椭圆于A、B两点,以OA、OB为邻边作平行四边形OAPB。 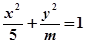 的离心率为
的离心率为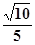 ,则实数
,则实数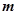 的值为___________.
的值为___________.