题目内容
椭圆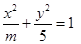 的焦距是2,则m的值为 ( )
的焦距是2,则m的值为 ( )
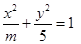 的焦距是2,则m的值为 ( )
的焦距是2,则m的值为 ( )| A.6 | B.9 | C.6或4 | D.9或1 |
C
分析:当焦点坐标在x轴时,c=
 =1,当焦点坐标在y轴时,c=
=1,当焦点坐标在y轴时,c=  =1,由此能得到实数m的值.
=1,由此能得到实数m的值.解:∵2c=2,∴c=1.
当焦点坐标在x轴时,
c=
 =1,
=1,∴m=6.
当焦点坐标在y轴时,
c=
 =1,
=1,∴m=4.
由此知,m=4或6.
故选C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
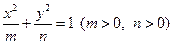 与曲线
与曲线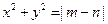 无交点,则椭圆的离心率
无交点,则椭圆的离心率 的取值范围是
的取值范围是
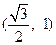
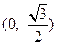
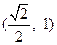

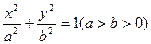 过点
过点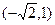 ,长轴长为
,长轴长为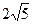 ,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.
,过点C(-1,0)且斜率为k的直线l与椭圆相交于不同的两点A、B.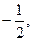 求直线l的斜率;
求直线l的斜率;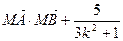 是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由.
是与k无关的常数?若存在,求出点M的坐标;若不存在,请说明理由.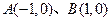 ,直线
,直线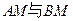 相交于点
相交于点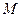 ,且它们的斜率之积为
,且它们的斜率之积为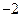 ,
,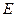 的方程;
的方程;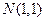 的直线
的直线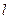 与曲线
与曲线 两点,且
两点,且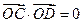 ,求直线
,求直线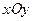 中,点M到点
中,点M到点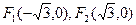 的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线
的距离之和是4,点M的轨迹是C与x轴的负半轴交于点A,不过点A的直线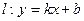 与轨迹C交于不同的两点P和Q.
与轨迹C交于不同的两点P和Q.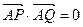 时,求k与b的关系,并证明直线
时,求k与b的关系,并证明直线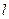 过定点.
过定点.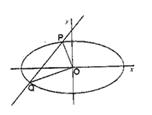
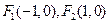 是椭圆C的两个焦点,
是椭圆C的两个焦点,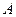 、
、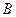 为过
为过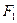 的直线与椭圆的交点,且
的直线与椭圆的交点,且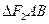 的周长为
的周长为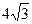 .
.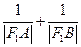 是否为定值,若是求出这个值,若不是说明理由.
是否为定值,若是求出这个值,若不是说明理由.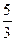 )的椭圆方程.
)的椭圆方程.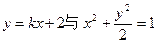 交于A、B两点,且
交于A、B两点,且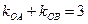 ,则直线AB的方程为: ( )
,则直线AB的方程为: ( )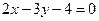 B、
B、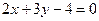
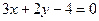 D、
D、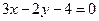
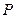 为椭圆上任一点(不是长轴顶点),过点
为椭圆上任一点(不是长轴顶点),过点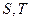 ,求证以线段
,求证以线段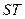 为直径的圆过这个椭圆的两个焦点
为直径的圆过这个椭圆的两个焦点