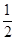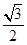题目内容
已知等差数列 的公差为2,若
的公差为2,若 成等比数列,则
成等比数列,则 =( )
=( )
A. | B. | C. | D. |
B
解析试题分析:直接利用a1,a3,a4成等比数列求出首项和公差的关系,再把公差代入即可求出a1.解:因为a1,a3,a4成等比数列,所以有a32=a1•a4⇒(a1+2d)2=a1•(a1+3d)⇒a1•d=-4d2,又因为d=2,所以a1=-8.故答案为:B
考点:等差数列与等比数列
点评:本题考查等差数列与等比数列的基础知识,考查方程思想在解决数列问题中的应用.在等差数列、等比数列问题中基本量是解题的关键,一般是根据已知条件把基本量求出来,然后在解决问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知等差数列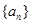 的前
的前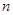 项和为
项和为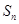 ,且
,且 则
则 ( )
( )
| A.11 | B.16 | C.20 | D.28 |
已知等差数列 中,
中, ,若
,若 ,则数列
,则数列 的前5项和等于( )
的前5项和等于( )
| A.30 | B.45 | C.90 | D.186 |
数列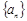 中,如果
中,如果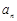 =
=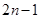 (n=1,2,3,…) ,那么这个数列是( ).
(n=1,2,3,…) ,那么这个数列是( ).
| A.公差为2的等差数列 | B.公差为-2的等差数列 |
| C.首项为-3的等差数列 | D.首项为-3的等比数列 |
在等差数列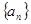 中,已知
中,已知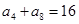 ,则
,则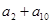 为 ( )
为 ( )
A.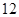 | B.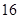 | C.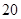 | D.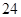 |
在数列 中,
中,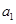 =1,
=1, ,则
,则 的值为 ( )
的值为 ( )
| A.99 | B.49 | C.102 | D.101 |
若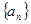 为等差数列,
为等差数列,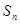 是其前n项的和,且
是其前n项的和,且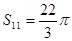 ,则
,则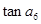 =( )
=( )
A.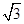 | B.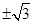 | C.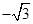 | D.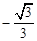 |
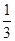 ,则D(3ξ-1)=( )
,则D(3ξ-1)=( )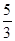 C、
C、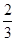 D、5
D、5  有两个不同的零点
有两个不同的零点 ,且方程
,且方程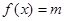 有两个不同的实根
有两个不同的实根 .若把这四个数按从小到大排列构成等差数列,则实数
.若把这四个数按从小到大排列构成等差数列,则实数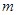 的值为
的值为