题目内容
已知等差数列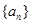 的前
的前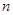 项和为
项和为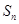 ,且
,且 则
则 ( )
( )
| A.11 | B.16 | C.20 | D.28 |
C
解析试题分析:由等差数列的性质知 成等差数列,所以有
成等差数列,所以有 ,解得
,解得 ,因此
,因此 .
.
考点:1.等差数列的性质;2.等差中项.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
在等差数列 中,
中, ,前n项的和是
,前n项的和是 ,则使
,则使 最大的项是( )
最大的项是( )
| A.第5项 | B.第6项 |
| C.第5项或第6项 | D.第6项或第7项 |
已知等差数列 的公差和首项都不等于0,且
的公差和首项都不等于0,且 ,
, ,
, 成等比数列,则
成等比数列,则 ( )
( )
| A.2 | B.3 | C.5 | D.7 |
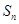 为等差数列
为等差数列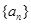 的前
的前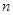 项和,
项和, ,
, ,正项等比数列
,正项等比数列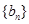 中,
中, ,
, ,则
,则 =( )
=( )
| A.8 | B.9 | C.10 | D.11 |
等差数列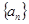 中的
中的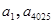 是函数
是函数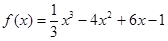 的极值点,则
的极值点,则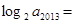 ( )
( )
A.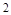 | B.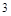 | C. | D.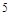 |
公差不为0的等差数列{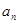 }的前21项的和等于前8项的和.若
}的前21项的和等于前8项的和.若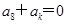 ,则k=( )
,则k=( )
| A.20 | B.21 | C.22 | D.23 |
在等差数列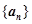 中,2a4+a7=3,则数列
中,2a4+a7=3,则数列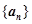 的前9项和等于( )
的前9项和等于( )
| A.9 | B.6 | C.3 | D.12 |
已知两个等差数列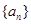 和
和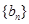 的前
的前 项和分别为A
项和分别为A 和
和 ,且
,且 ,则使得
,则使得 为整数的正整数
为整数的正整数 的个数是( )
的个数是( )
| A.2 | B.3 | C.4 | D.5 |
已知等差数列 的公差为2,若
的公差为2,若 成等比数列,则
成等比数列,则 =( )
=( )
A. | B. | C. | D. |