题目内容
(本小题满分为14分)
已知抛物线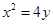 的焦点为F,A、B是热线上的两动点,且
的焦点为F,A、B是热线上的两动点,且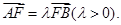 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。
(I)证明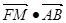 为定值;
为定值;
(II)设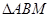 的面积为S,写出
的面积为S,写出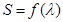 的表达式,并求S的最小值。
的表达式,并求S的最小值。
已知抛物线
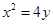 的焦点为F,A、B是热线上的两动点,且
的焦点为F,A、B是热线上的两动点,且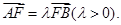 过A、B两点分别作抛物线的切线,设其交点为M。
过A、B两点分别作抛物线的切线,设其交点为M。(I)证明
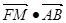 为定值;
为定值;(II)设
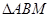 的面积为S,写出
的面积为S,写出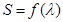 的表达式,并求S的最小值。
的表达式,并求S的最小值。(Ⅰ)由已知条件,得F(0,1),

设
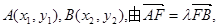
即得
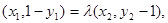
∴

将①式两边平方并把
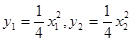 代入得
代入得 ③
③解②、③式得
 且有
且有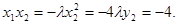
抛物线方程为
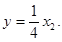
求导得
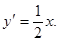
所以过抛物线上A、B两点的切线方程分别是
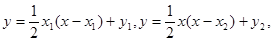
即

解出两条切线的交点M的坐标为
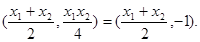 ……4分
……4分所以
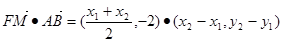
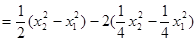
所以
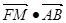 为定值,其值为0。 ……7分
为定值,其值为0。 ……7分 (Ⅱ)由(Ⅰ)知在△ABM中,FM⊥AB,因而S=
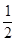 |AB||FM|。
|AB||FM|。|FM|


因为|AF|、|BF|分别等于A、B到抛物线准线y= -1的距离,所以
|AB|=|AF|+|BF|
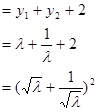
于是

 ……11分
……11分由

且当
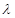 =1时,S取得最小值4, ……14分
=1时,S取得最小值4, ……14分略

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
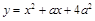 的切线,当
的切线,当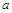 变化时,两个切点分别在抛物线( )上
变化时,两个切点分别在抛物线( )上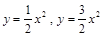
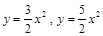
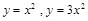
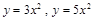
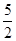
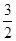
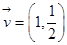 为方向向量的直线
为方向向量的直线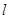 过点
过点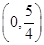 ,抛物线C:
,抛物线C: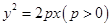 的顶点关于直线
的顶点关于直线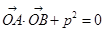 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程. 上纵坐标为
上纵坐标为 的点
的点 到焦点的距离为2.
到焦点的距离为2.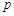 的值;
的值;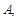

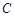 为抛物线上三点,且线段
为抛物线上三点,且线段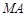 ,
, ,
,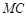 与
与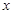 轴交点的横坐标依次组成公差为1的等差数列,若
轴交点的横坐标依次组成公差为1的等差数列,若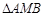 的面积是
的面积是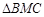 面积的
面积的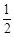 ,求直线
,求直线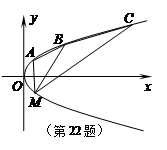
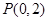 的直线
的直线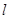 与抛物线
与抛物线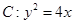 交于
交于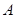 、
、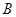 两点,
两点,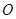 为坐标原点.
为坐标原点.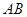 为直径的圆经过原点
为直径的圆经过原点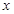 轴于点
轴于点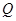 ,求
,求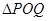 面积的取值范围.
面积的取值范围. 系中,已知点
系中,已知点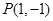 ,过点
,过点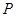 作抛物线
作抛物线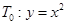 的切线,其切点分别为
的切线,其切点分别为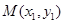 、
、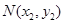 (其中
(其中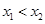 ).
).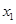 与
与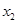 的值;
的值;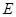 与直线
与直线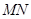 相切,求圆
相切,求圆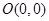 作圆
作圆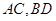 ,求四边形
,求四边形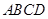 面积的最大值.
面积的最大值.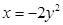 的准线方程是 ( )
的准线方程是 ( )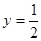
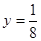
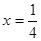
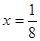
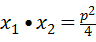 是P1P2过抛物线焦点的( )
是P1P2过抛物线焦点的( )