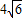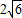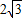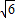题目内容
在相距4千米的A,B两点处测量目标C,若∠CAB=60°,∠CBA=75°,则B,C两点之间的距离是多少千米.( )
分析:先由B点向AC作垂线,垂足为D,设BC=x,利用三角形内角和求得∠ACB,进而表示出AD,进而在Rt△ABD中,表示出AB和AD的关系求得x.
解答: 解:由B点向AC作垂线,垂足为D,设BC=x,
解:由B点向AC作垂线,垂足为D,设BC=x,
∵∠CAB=60°,∠CBA=75°
∴∠ACB=180°-75°-60°=45°
∴AD=
x
∴在Rt△ABD中,AB•sin60°=
x
x=2
(千米),
即B、C两点之间的距离为2
千米.
故答案为:2
.
 解:由B点向AC作垂线,垂足为D,设BC=x,
解:由B点向AC作垂线,垂足为D,设BC=x,∵∠CAB=60°,∠CBA=75°
∴∠ACB=180°-75°-60°=45°
∴AD=
| ||
| 2 |
∴在Rt△ABD中,AB•sin60°=
| ||
| 2 |
x=2
| 6 |
即B、C两点之间的距离为2
| 6 |
故答案为:2
| 6 |
点评:本题主要考查了解三角形的实际应用.主要是利用了三角形中45°和60°这两个特殊角,建立方程求得BC即可.

练习册系列答案
相关题目
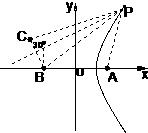 舰A在舰B的正东6千米处,舰C在舰B的北偏西30°且与B相距4千米,它们准备捕海洋动物,某时刻A发现动物信号,4秒后B、C同时发现这种信号,A发射麻醉炮弹 设舰与动物均为静止的,动物信号的传播速度为1千米/秒,若不计空气阻力与舰高,问舰A发射炮弹的方位角应是多少?
舰A在舰B的正东6千米处,舰C在舰B的北偏西30°且与B相距4千米,它们准备捕海洋动物,某时刻A发现动物信号,4秒后B、C同时发现这种信号,A发射麻醉炮弹 设舰与动物均为静止的,动物信号的传播速度为1千米/秒,若不计空气阻力与舰高,问舰A发射炮弹的方位角应是多少?