题目内容
18. 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB>1,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为2$\sqrt{2}$.则该长方体外接球的表面积为6π.
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB>1,点E在棱AB上移动,小蚂蚁从点A沿长方体的表面爬到点C1,所爬的最短路程为2$\sqrt{2}$.则该长方体外接球的表面积为6π.
分析 根据四边形ADD1A是正方形,则小蚂蚁从点A沿长方体的表面爬到点C1可能有两种途径,然后比较两个路程的大小从而求出AB的长,从而求得该长方体外接球的表面积.
解答 解:(1)设AB=x,点A到点C1可能有两种途径,如图甲的最短路程为|AC1|=$\sqrt{{x}^{2}+4}$.
如图乙的最短路程为|AC1|=$\sqrt{{x}^{2}+2x+2}$,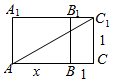
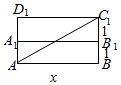
图甲 图乙
∵x>1,∴x2+2x+2>x2+2+2=x2+4,故从点A沿长方体的表面爬到点C1的最短距离为$\sqrt{{x}^{2}+4}$=2$\sqrt{2}$
解得x=2.即AB的长度为2.
设长方体外接球的半径为R,则(2R)2=12+12+22=6,
∴R2=$\frac{3}{2}$,∴S表=4πR2=6π.
即该长方体外接球的表面积为6π.
故答案为:6π
点评 本题考查棱柱的结构特征,考查分类讨论思想,考查计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.等差数列{an}中,a2+a4=2,a3+a5=8,那么它的公差是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a、b分别为2、1,则输出的n=( )
宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若输入的a、b分别为2、1,则输出的n=( ) 如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,∠CC1B1=$\frac{2π}{3}$,AB=BB1=2,BC=1,D为CC1的中点.
如图,在三棱柱ABC-A1B1C1中,AB⊥平面BB1C1C,∠CC1B1=$\frac{2π}{3}$,AB=BB1=2,BC=1,D为CC1的中点.