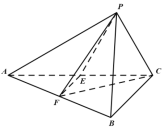
题目内容
【题目】设有下列四个命题：
p1：两两相交且不过同一点的三条直线必在同一平面内.
p2：过空间中任意三点有且仅有一个平面.
p3：若空间两条直线不相交，则这两条直线平行.
p4：若直线l
平面α，直线m⊥平面α，则m⊥l.
则下述命题中所有真命题的序号是__________.
①
②
③
④
【答案】①③④
【解析】
利用两交线直线确定一个平面可判断命题
的真假；利用三点共线可判断命题
的真假；利用异面直线可判断命题
的真假，利用线面垂直的定义可判断命题
的真假.再利用复合命题的真假可得出结论.
对于命题，可设
与
相交，这两条直线确定的平面为
；
若
与相交，则交点
在平面内，
同理，与的交点
也在平面内，
所以，
，即
，命题为真命题；
对于命题，若三点共线，则过这三个点的平面有无数个，
命题为假命题；
对于命题，空间中两条直线相交、平行或异面，
命题为假命题；
对于命题，若直线
平面，
则
垂直于平面内所有直线，
直线
平面，
直线直线
，
命题为真命题.
综上可知，
，
为真命题，
，
为假命题，
为真命题，
为假命题，
为真命题，
为真命题.
故答案为：①③④.
【题目】某学生兴趣小组随机调查了某市100天中每天的空气质量等级和当天到某公园锻炼的人次，整理数据得到下表（单位：天）：
锻炼人次 空气质量等级 | [0，200] | (200，400] | (400，600] |
1（优） | 2 | 16 | 25 |
2（良） | 5 | 10 | 12 |
3（轻度污染） | 6 | 7 | 8 |
4（中度污染） | 7 | 2 | 0 |
（1）分别估计该市一天的空气质量等级为1，2，3，4的概率；
（2）求一天中到该公园锻炼的平均人次的估计值（同一组中的数据用该组区间的中点值为代表）；
（3）若某天的空气质量等级为1或2，则称这天“空气质量好”；若某天的空气质量等级为3或4，则称这天“空气质量不好”．根据所给数据，完成下面的2×2列联表，并根据列联表，判断是否有95%的把握认为一天中到该公园锻炼的人次与该市当天的空气质量有关？
人次≤400 | 人次>400 | |
空气质量好 | ||
空气质量不好 |
附：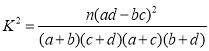
，
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
