题目内容
(13分)(2011•天津)设椭圆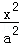 +
+ =1(a>b>0)的左、右焦点分别为F1,F2.点P(a,b)满足|PF2|=|F1F2|.
=1(a>b>0)的左、右焦点分别为F1,F2.点P(a,b)满足|PF2|=|F1F2|.
(Ⅰ)求椭圆的离心率e;
(Ⅱ)设直线PF2与椭圆相交于A,B两点,若直线PF2与圆(x+1)2+ =16相交于M,N两点,且|MN|=
=16相交于M,N两点,且|MN|= |AB|,求椭圆的方程.
|AB|,求椭圆的方程.
(Ⅰ) (Ⅱ)
(Ⅱ) +
+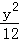 =1
=1
解析试题分析:(Ⅰ)直接利用|PF2|=|F1F2|,对应的方程整理后即可求椭圆的离心率e;
(Ⅱ)先把直线PF2与椭圆方程联立求出A,B两点的坐标以及对应的|AB|两点,进而求出|MN|,再利用弦心距,弦长以及圆心到直线的距离之间的等量关系,即可求椭圆的方程.
解:(Ⅰ)设F1(﹣c,0),F2(c,0) (c>0).
由题得|PF2|=|F1F2|,即 =2c,整理得2
=2c,整理得2 +
+ ﹣1=0,得
﹣1=0,得 =﹣1(舍),或
=﹣1(舍),或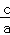 =
= ,
,
所以e= .
.
(Ⅱ)由(Ⅰ)知a=2c,b= c,可得椭圆方程为3x2+4y2=12c2,直线方程PF2为y=
c,可得椭圆方程为3x2+4y2=12c2,直线方程PF2为y= (x﹣c).
(x﹣c).
A,B的坐标满足方程组 ,
,
消y并整理得5x2﹣8xc=0,
解得x=0,x= ,得方程组的解为
,得方程组的解为 ,
, ,
,
不妨设A( c,
c,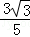 c),B(0,﹣
c),B(0,﹣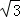 c).
c).
所以|AB|=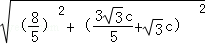 =
= c,于是|MN|=
c,于是|MN|= |AB|=2c.
|AB|=2c.
圆心(﹣1,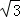 )到直线PF2的距离d=
)到直线PF2的距离d= ,
,
因为d2+ =42,所以
=42,所以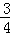 (2+c)2+c2=16,整理得c=﹣
(2+c)2+c2=16,整理得c=﹣ (舍)或c=2.
(舍)或c=2.
所以椭圆方程为 +
+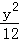 =1.
=1.
点评:本题主要考查椭圆的方程和几何性质,直线的方程,两点间的距离公式以及点到直线的距离公式等基础知识,考查用代数方法研究圆锥曲线的性质和数形结合的数学思想,考查解决问题的能力和运算能力.

练习册系列答案
相关题目
 的焦点
的焦点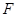 的直线交抛物线于
的直线交抛物线于 ,
, 两点.求证:
两点.求证: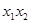 为定值;
为定值;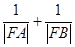 为定值.
为定值.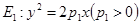 和
和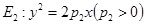 ,过原点
,过原点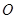 的两条直线
的两条直线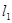 和
和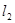 ,
, 分别交于
分别交于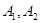 两点,
两点,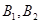 两点.
两点.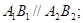
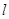 (异于
(异于 两点.记
两点.记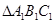 与
与 的面积分别为
的面积分别为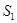 与
与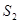 ,求
,求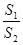 的值.
的值.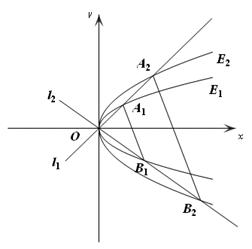
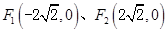 ,长轴长为6,
,长轴长为6, ,一条准线的方程为x=2
,一条准线的方程为x=2 .
.
 ,其中M,N是椭圆上的点.直线OM与ON的斜率之积为﹣
,其中M,N是椭圆上的点.直线OM与ON的斜率之积为﹣ .
.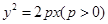 上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.
上的点M分别向C的准线和x轴作垂线,两条垂线及C的准线和x轴围成边长为4的正方形,点M在第一象限.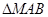 的面积.
的面积. :
: 的左顶点为
的左顶点为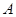 ,直线
,直线 交椭圆
交椭圆 两点(
两点( 上
上 下),动点
下),动点 和定点
和定点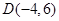 都在椭圆
都在椭圆 的面积.
的面积. 为梯形,求点
为梯形,求点 为实数,
为实数, ,求
,求 的最大值.
的最大值. 为椭圆C:
为椭圆C:
 的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率
的左、右焦点,D,E是椭圆的两个顶点,椭圆的离心率 ,
, 的面积为
的面积为 .若点
.若点 在椭圆C上,则点
在椭圆C上,则点 称为点M的一个“椭圆”,直线
称为点M的一个“椭圆”,直线 与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
与椭圆交于A,B两点,A,B两点的“椭圆”分别为P,Q.
 的直线
的直线 的焦点为
的焦点为 ,点
,点 是椭圆
是椭圆 上的一点,
上的一点, 与
与 轴的交点
轴的交点 恰为
恰为 .
. 为椭圆的右顶点,过焦点
为椭圆的右顶点,过焦点 的直线与椭圆
的直线与椭圆 ,求
,求 面积的取值范围.
面积的取值范围.