题目内容
3. 如图,AB为圆O的直径,E是圆O上不同于A、B的动点,四边形ABCD为矩形,平面ABCD⊥平面ABE,F是DE的中点.
如图,AB为圆O的直径,E是圆O上不同于A、B的动点,四边形ABCD为矩形,平面ABCD⊥平面ABE,F是DE的中点.(Ⅰ)求证:OF∥平面BCE;
(Ⅱ)平面ADE⊥平面BCE.
分析 (Ⅰ)根据线面平行的判定定理即可证明OF∥平面BCE;
(Ⅱ)根据面面垂直的判定定理即可证明平面ADE⊥平面BCE.
解答 证明:(Ⅰ)取CE的中点G,连接FG,BG,
∵F为DE的中点,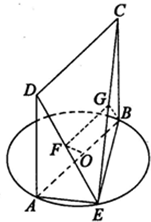
∴FG∥CD且FG=$\frac{1}{2}$CD,
∵ABCD为矩形,且O为AB的中点,
∴OB∥CD,且OB=$\frac{1}{2}$CD,
∴OB∥FG,且OB=FG,
∴OFGB为平行四边形,
∴OF∥GB,
∵OF?平面BCD,GB?平面BCE,
∴OF∥平面BCE.
(Ⅱ)由平面ABCD⊥平面ABE,且平面ABCD∩平面ABE=AB,
DA⊥AB,DA?平面ABCD,
∴DA⊥平面ABE,
∴BE⊥AE,
∴BE⊥平面DAE,
∵BE?平面BCE,
∴平面ADE⊥平面BCE.
点评 本题主要考查空间直线和平面平行以及面面垂直的判定,利用相应的判定定理是解决本题的关键.

练习册系列答案
相关题目
11. 如图,在三棱柱ABC-A1B1C1中,B1C⊥AB,侧面BCC1B1为菱形.
如图,在三棱柱ABC-A1B1C1中,B1C⊥AB,侧面BCC1B1为菱形.
(1)求证:平面ABC1⊥平面BCC1B1;
(2)如果点D,E分别为A1C1,BB1的中点,求证:DE∥平面ABC1.
 如图,在三棱柱ABC-A1B1C1中,B1C⊥AB,侧面BCC1B1为菱形.
如图,在三棱柱ABC-A1B1C1中,B1C⊥AB,侧面BCC1B1为菱形.(1)求证:平面ABC1⊥平面BCC1B1;
(2)如果点D,E分别为A1C1,BB1的中点,求证:DE∥平面ABC1.