题目内容
已知函数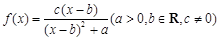 ,函数
,函数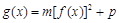 (
(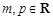 ,且mp<0),给出下列结论:
,且mp<0),给出下列结论:
①存在实数r和s,使得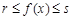 对于任意实数x恒成立;
对于任意实数x恒成立;
②函数 的图像关于点
的图像关于点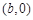 对称;
对称;
③函数 可能不存在零点(注:使关于x的方程
可能不存在零点(注:使关于x的方程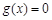 的实数x叫做函数
的实数x叫做函数 的零点);
的零点);
④关于x的方程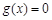 的解集可能为{-1,1,4,5}.
的解集可能为{-1,1,4,5}.
其中正确结论的序号为 (写出所有正确结论的序号).
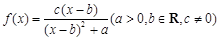 ,函数
,函数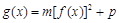 (
(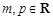 ,且mp<0),给出下列结论:
,且mp<0),给出下列结论:①存在实数r和s,使得
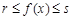 对于任意实数x恒成立;
对于任意实数x恒成立;②函数
 的图像关于点
的图像关于点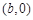 对称;
对称;③函数
 可能不存在零点(注:使关于x的方程
可能不存在零点(注:使关于x的方程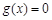 的实数x叫做函数
的实数x叫做函数 的零点);
的零点);④关于x的方程
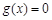 的解集可能为{-1,1,4,5}.
的解集可能为{-1,1,4,5}.其中正确结论的序号为 (写出所有正确结论的序号).
①③
(1)函数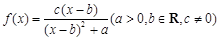 的定义域为
的定义域为 。
。
令 ,得
,得 ,
, 。
。
当 时,
时, ;
;
当 时,∵
时,∵ ,
, ,∴
,∴ ,当且仅当
,当且仅当 ,即
,即 时,
时, ,故存在实数
,故存在实数 和
和 ,使得
,使得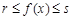 对于任意实数x恒成立,故结论①正确。
对于任意实数x恒成立,故结论①正确。
(2)设 为函数
为函数 图像上的任意一点,
图像上的任意一点, 关于点
关于点 的对称点为
的对称点为 ,则
,则 ,
,
所以 ,
,
知点 不在函数
不在函数 的图像上,故函数
的图像上,故函数 的图像不关于点
的图像不关于点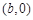 对称,结论②不正确。
对称,结论②不正确。
(3)令 ,得
,得 ,当
,当 时,由(1)知,方程
时,由(1)知,方程 无解,即函数
无解,即函数 不存在零点,故结论③正确。
不存在零点,故结论③正确。
(4)由(2)知,函数 的图像关于直线
的图像关于直线 对称,则关于x的方程
对称,则关于x的方程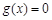 的解关于
的解关于 对称,但
对称,但 ,结论④不正确。
,结论④不正确。
综上,正确结论的序号为①③。
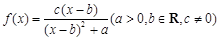 的定义域为
的定义域为 。
。令
 ,得
,得 ,
, 。
。当
 时,
时, ;
;当
 时,∵
时,∵ ,
, ,∴
,∴ ,当且仅当
,当且仅当 ,即
,即 时,
时, ,故存在实数
,故存在实数 和
和 ,使得
,使得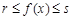 对于任意实数x恒成立,故结论①正确。
对于任意实数x恒成立,故结论①正确。(2)设
 为函数
为函数 图像上的任意一点,
图像上的任意一点, 关于点
关于点 的对称点为
的对称点为 ,则
,则 ,
,所以
 ,
,知点
 不在函数
不在函数 的图像上,故函数
的图像上,故函数 的图像不关于点
的图像不关于点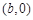 对称,结论②不正确。
对称,结论②不正确。(3)令
 ,得
,得 ,当
,当 时,由(1)知,方程
时,由(1)知,方程 无解,即函数
无解,即函数 不存在零点,故结论③正确。
不存在零点,故结论③正确。(4)由(2)知,函数
 的图像关于直线
的图像关于直线 对称,则关于x的方程
对称,则关于x的方程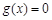 的解关于
的解关于 对称,但
对称,但 ,结论④不正确。
,结论④不正确。综上,正确结论的序号为①③。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
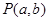 与点
与点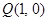 在直线
在直线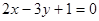 的两侧,则下列说法: ①
的两侧,则下列说法: ① 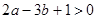 ; ②
; ② 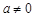 时,
时,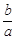 有最小值,无最大值;
有最小值,无最大值;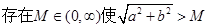 恒成立;
恒成立;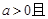
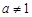 ,
,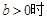 , 则
, 则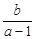 的取值范围为(-
的取值范围为(-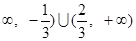 ;
;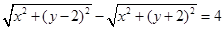 的点P(x,y)的轨迹是双曲线
的点P(x,y)的轨迹是双曲线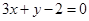 的距离等于到点P(1,-1)的距离的点的轨迹为抛物线
的距离等于到点P(1,-1)的距离的点的轨迹为抛物线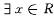 ,使得
,使得
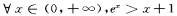
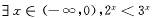
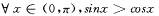
 x∈
x∈ ,ex > 0”的否定是
,ex > 0”的否定是 x∈
x∈ ”的否定是“
”的否定是“ ”;
”; ,则
,则 或
或 ;
; 是奇数.
是奇数.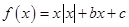 ,给出下列4个命题:
,给出下列4个命题: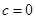 时,
时,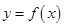 是奇函数;2,
是奇函数;2,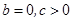 时,方程
时,方程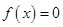 只有一个实根;
只有一个实根;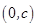 对称;4,方程
对称;4,方程 ,则
,则 ”的逆命题是____________________
”的逆命题是____________________