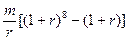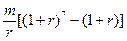题目内容
已知数列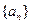 各项均为正数,其前
各项均为正数,其前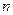 项和
项和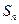 满足
满足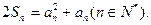
(1)证明: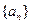 为等差数列
为等差数列
(2)令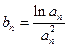 ,记
,记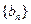 的前
的前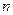 项和为
项和为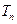 ,求证:
,求证: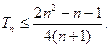
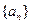 各项均为正数,其前
各项均为正数,其前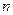 项和
项和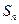 满足
满足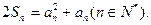
(1)证明:
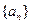 为等差数列
为等差数列(2)令
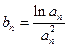 ,记
,记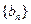 的前
的前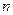 项和为
项和为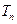 ,求证:
,求证: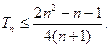
解:(1)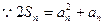
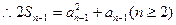
两式相减得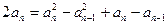
整理得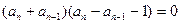
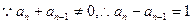 (常数)
(常数)
又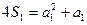
即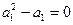 ,解得
,解得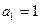
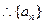 是以1为首项1为公差的等差数列 6分
是以1为首项1为公差的等差数列 6分
(2)方法一、由(1)知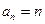
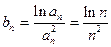
即证: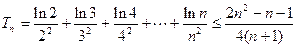
设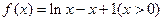 ,
,
则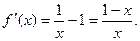
当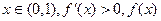 为单调递增函数,
为单调递增函数,
当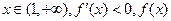 单调递减函数;
单调递减函数;
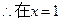 处
处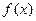 取得极大值,也取得最大值。
取得极大值,也取得最大值。
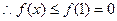 即
即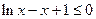
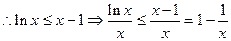
 时,令
时,令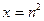 ,得
,得
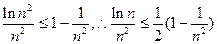
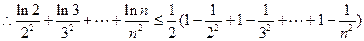
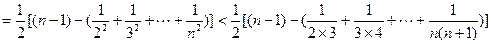
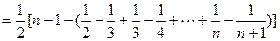
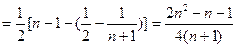
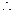 当
当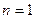 ,有
,有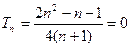
故结论成立。 13分
方法二:由(1)知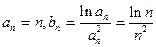
当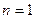 时,
时,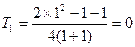 成立,
成立,
当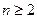 时,即证:
时,即证: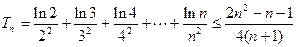
令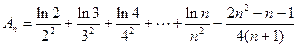
即证: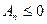
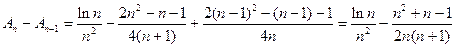
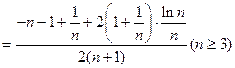
当 时,容易证明
时,容易证明 单减,
单减,
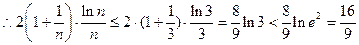
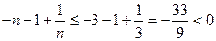
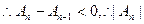 单减,
单减,
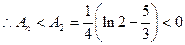
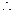 结论成立 13分
结论成立 13分
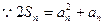
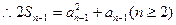
两式相减得
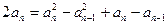
整理得
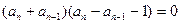
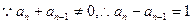 (常数)
(常数)又
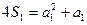
即
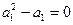 ,解得
,解得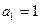
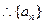 是以1为首项1为公差的等差数列 6分
是以1为首项1为公差的等差数列 6分(2)方法一、由(1)知
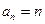
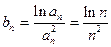
即证:
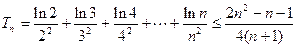
设
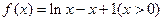 ,
,则
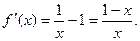
当
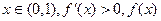 为单调递增函数,
为单调递增函数,当
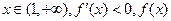 单调递减函数;
单调递减函数;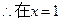 处
处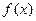 取得极大值,也取得最大值。
取得极大值,也取得最大值。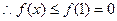 即
即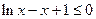
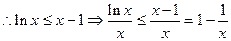
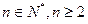 时,令
时,令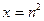 ,得
,得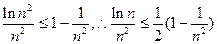
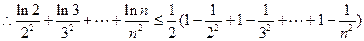
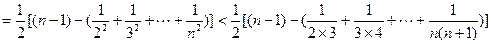
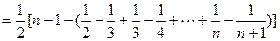
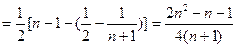
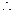 当
当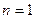 ,有
,有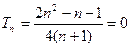
故结论成立。 13分
方法二:由(1)知
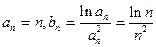
当
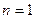 时,
时,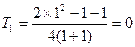 成立,
成立,当
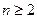 时,即证:
时,即证: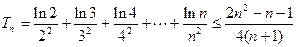
令
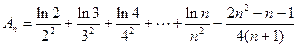
即证:
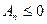
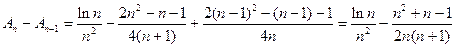
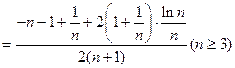
当
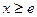 时,容易证明
时,容易证明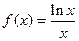 单减,
单减,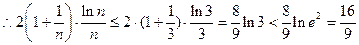
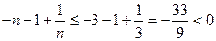
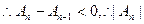 单减,
单减,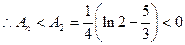
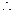 结论成立 13分
结论成立 13分
练习册系列答案
相关题目
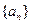 中,
中,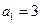 ,
,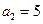 ,其前
,其前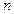 项和
项和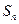 满足
满足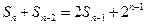
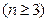 ,令
,令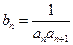 .
.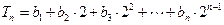 ,求证:
,求证: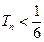 ;
; 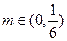 ,均存在
,均存在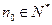 ,使得
,使得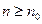 时,
时,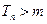 .
.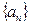 的公差为
的公差为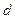 ,且
,且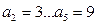 ,数列
,数列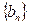 的前
的前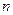 项和为
项和为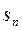 ,且
,且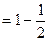
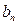
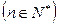

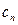 =
=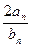 求证:数列
求证:数列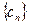 的前
的前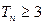 。
。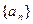 是等差数列,
是等差数列,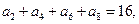 求
求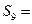 _______.
_______.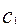 ,
,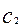 ...,
...,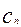 ,...是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=
,...是坐标平面上的一列圆,它们的圆心都在x轴的正半轴上,且都与直线y=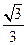 x相切,对每一个正整数n,圆
x相切,对每一个正整数n,圆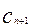 相互外切,以
相互外切,以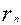 表示
表示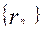 为递增数列.
为递增数列.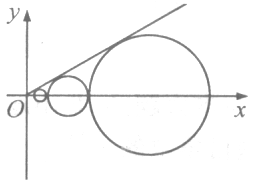
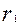 =1,求数列错误!不能通过编辑域代码创建对象。的前n项和.
=1,求数列错误!不能通过编辑域代码创建对象。的前n项和.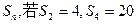 ,则该数列的公差d= 。
,则该数列的公差d= 。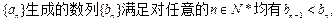
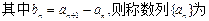 “Z数列”
“Z数列”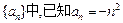 ,试判断数列
,试判断数列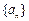 是否为“Z数列”;
是否为“Z数列”;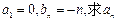 ;
;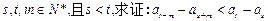 。
。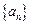 的通项公式为
的通项公式为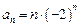 ,则数列
,则数列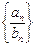 成等比数列是数列
成等比数列是数列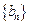 的通项公式为
的通项公式为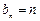 的( ▲ )
的( ▲ )