题目内容
如图1-23,矩形ABCD中,M为BC中点,DM⊥AC于E,求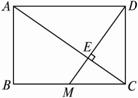
图1-23
思路分析:由题意,考虑射影定理,有CD2=DE·DM,CM2=ME·MD,在条件“M为BC中点”下,要求![]() ,即求
,即求![]() .根据三角形相似解决即可.
.根据三角形相似解决即可.
解:∵DM⊥AC,M为BC中点,?
∴在矩形ABCD中,△MEC∽△DEA.?
∴![]() =
=![]() =
=![]() .?
.?
设ME =k,则DE =2k,?
∴在Rt△DCM中,∵CE⊥DM,?
∴MC2=ME·MD =k·3k =3k2,?
BC2=(2MC)2=4×3k2=12k2,?
![]() .?
.?
同理, ![]() .
.
∴![]() =
=![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
如图,在矩形ABCD中,BD为对角线,AE⊥BD,AB=
,AD=1,则BE=( )

| 2 |

| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
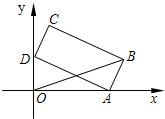 如图,矩形的长
如图,矩形的长
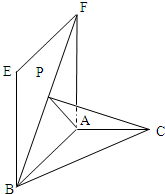 (2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=
(2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=