题目内容
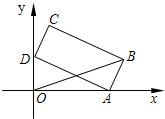 如图,矩形的长AD=2
如图,矩形的长AD=2| 3 |
分析:过点B作BH⊥OA,垂足为H.设∠OAD=θ进而表示出∠BAH和OA,HB,AH,然后利用勾股定理求得OB的解析式,利用θ的范围确定OB2最大值.
解答: 解:过点B作BH⊥OA,垂足为H.
解:过点B作BH⊥OA,垂足为H.
设∠OAD=θ,则∠BAH=
-θ.
OA=2
cosθ,BH=sin(
-θ)=cosθ,
AH=cos(
-θ)=sinθ.
OB2=(2
cosθ+sinθ)2+cos2θ
=7+6cos2θ+2
sin2θ.
=7+4
sin(2θ+
)
由0<θ<
知
<2θ+
<
,
所以,当θ=
时,OB2取得最大值7+4
.
 解:过点B作BH⊥OA,垂足为H.
解:过点B作BH⊥OA,垂足为H.设∠OAD=θ,则∠BAH=
| π |
| 2 |
OA=2
| 3 |
| π |
| 2 |
AH=cos(
| π |
| 2 |
OB2=(2
| 3 |
=7+6cos2θ+2
| 3 |
=7+4
| 3 |
| π |
| 3 |
由0<θ<
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
所以,当θ=
| π |
| 12 |
| 3 |
点评:本题主要考查了解三角形的实际应用.解题的关键是根据题意建立三角函数模型,借助三角函数的基本性质解决问题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
 如图,矩形ORTM内放置5个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则
如图,矩形ORTM内放置5个边长均为1的小正方形,其中A,B,C,D在矩形的边上,且E为AD的中点,则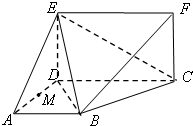 如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.
如图所示的多面体中,已知直角梯形ABCD和矩形CDEF所在的平面互相垂直,AD⊥DC,AB∥DC,AB=AD=DE=4,CD=8.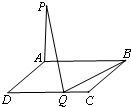 如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是
如图,矩形ABCD的长AB=2,宽AD=x,若PA⊥平面ABCD,矩形的边CD上至少有一个点Q,使得PQ⊥BQ,则x的范围是 某小区规划一块周长为2a(a为正常数)的矩形停车场,其中如图所示的直角三角形ADP内为绿化区域.且∠PAC=∠CAB.设矩形的长AB=x,AB>AD
某小区规划一块周长为2a(a为正常数)的矩形停车场,其中如图所示的直角三角形ADP内为绿化区域.且∠PAC=∠CAB.设矩形的长AB=x,AB>AD