题目内容
已知A(3,0),B(0,3)C(cosα,sinα),O为原点.
(1)若 ∥
∥ ,求tanα的值;
,求tanα的值;
(2)若
 ,求sin2α的值.
,求sin2α的值.
(3)若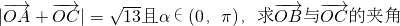 .
.
解:(1)∵A(3,0),B(0,3),C(cosα,sinα),
∴ =(cosα,sinα),
=(cosα,sinα), =(-3,3),
=(-3,3),
∵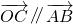 ,∴3cosα+3sinα=0,解得tanα=-1
,∴3cosα+3sinα=0,解得tanα=-1
(2)由题意得, =(coaα-3,sinα),
=(coaα-3,sinα), =(coaα,sinα-3),
=(coaα,sinα-3),
∵ ⊥
⊥ ,∴coaα(coaα-3)+sinα(sinα-3)=0,
,∴coaα(coaα-3)+sinα(sinα-3)=0,
1-3(sinα+coaα)=0,即sinα+coaα= ,
,
两边平方后得,sin2α=- ,
,
(3)由题意得, =(3,0),
=(3,0), =(cosα,sinα),
=(cosα,sinα),
∴ =(coaα+3,sinα),由|
=(coaα+3,sinα),由| |=
|= 得,
得,
(cosα+3)2+sin2α=13,即cosα= ,则α=
,则α= ,
,
∴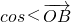 ,
,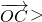 =
= =
= =
= ,
,
则所求的向量的夹角是 .
.
分析:(1)根据条件求出向量 和
和 的坐标,利用向量共线的坐标表示以及商的关系,,求出tanα的值;
的坐标,利用向量共线的坐标表示以及商的关系,,求出tanα的值;
(2)根据条件求出向量 和
和 的坐标,利用
的坐标,利用 列出方程,再由倍角的正弦公式和平方关系求出sin2α的值;
列出方程,再由倍角的正弦公式和平方关系求出sin2α的值;
(3)求出对应向量的坐标,再由| |=
|= 求出α的值,利用向量的数量积运算求出所求向量夹角的余弦值,根据夹角的范围求出角的度数.
求出α的值,利用向量的数量积运算求出所求向量夹角的余弦值,根据夹角的范围求出角的度数.
点评:本题考查两个向量的数量积公式的应用,两个向量垂直的性质,两个向量共线的性质,主要利用两个向量坐标形式进行运算求解,注意向量夹角的范围.
∴
 =(cosα,sinα),
=(cosα,sinα), =(-3,3),
=(-3,3),∵
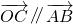 ,∴3cosα+3sinα=0,解得tanα=-1
,∴3cosα+3sinα=0,解得tanα=-1(2)由题意得,
 =(coaα-3,sinα),
=(coaα-3,sinα), =(coaα,sinα-3),
=(coaα,sinα-3),∵
 ⊥
⊥ ,∴coaα(coaα-3)+sinα(sinα-3)=0,
,∴coaα(coaα-3)+sinα(sinα-3)=0,1-3(sinα+coaα)=0,即sinα+coaα=
 ,
,两边平方后得,sin2α=-
 ,
,(3)由题意得,
 =(3,0),
=(3,0), =(cosα,sinα),
=(cosα,sinα),∴
 =(coaα+3,sinα),由|
=(coaα+3,sinα),由| |=
|= 得,
得,(cosα+3)2+sin2α=13,即cosα=
 ,则α=
,则α= ,
,∴
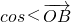 ,
,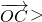 =
= =
= =
= ,
,则所求的向量的夹角是
 .
.分析:(1)根据条件求出向量
 和
和 的坐标,利用向量共线的坐标表示以及商的关系,,求出tanα的值;
的坐标,利用向量共线的坐标表示以及商的关系,,求出tanα的值;(2)根据条件求出向量
 和
和 的坐标,利用
的坐标,利用 列出方程,再由倍角的正弦公式和平方关系求出sin2α的值;
列出方程,再由倍角的正弦公式和平方关系求出sin2α的值;(3)求出对应向量的坐标,再由|
 |=
|= 求出α的值,利用向量的数量积运算求出所求向量夹角的余弦值,根据夹角的范围求出角的度数.
求出α的值,利用向量的数量积运算求出所求向量夹角的余弦值,根据夹角的范围求出角的度数.点评:本题考查两个向量的数量积公式的应用,两个向量垂直的性质,两个向量共线的性质,主要利用两个向量坐标形式进行运算求解,注意向量夹角的范围.

练习册系列答案
相关题目