题目内容

若函数f（x）=log_a（2-ax）（a＞0a≠1）在区间（1，3）内单调递增，则a的取值范围是

A.
[ $数学公式$ ，1）
B.
（0， $数学公式$ ]
C.
（1， $数学公式$ ）
D.
[ $数学公式$ ）

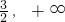B
分析：先将函数f（x）=log_a（2-ax）转化为y=log_at，t=2-ax，两个基本函数，再利用复合函数求解．
解答：解：令y=log_at，t=2-ax，
∵a＞0
∴t=2-ax在（1，3）上单调递减
∵f（x）=log_a（2-ax）（a＞0a≠1）在区间（1，3）内单调递增
∴函y=log_at是减函数，且t（x）＞0在（1，3）上成立
∴ $\text{[math]}$
∴0＜a≤ $\text{[math]}$
故选B．
点评：本题主要考查复合函数，关键是分解为两个基本函数，利用同增异减的结论研究其单调性，再求参数的范围．本题容易忽视t=2-ax＞0的情况导致出错．

练习册系列答案

高中金牌单元测试系列答案

名师一号高中同步学习方略系列答案

华夏1卷通系列答案

课时方案新版新理念导学与测评系列答案

课堂金考卷创优单元测评系列答案

名师伴你行高中同步导学案系列答案

名师新课堂集优360度系列答案

名师指导考出好成绩系列答案

期末第1卷系列答案

相关题目

若函数f(x)＝的定义域为M，g(x)＝lo(2＋x＝6x²)的单调递减区间是开区间N，设全集U＝R，则M∩C_U(N)＝________．

函数f(x)＝lo(x²－2ax＋3)．

(1)若f(x)的定义域为R，值域为(－∞，－1]，试求实数a的值；

(2)若f(x)在(－∞，1]内是增函数，试求实数a的取值范围．

已知函数(m∈R)

(1)若y＝lo[8－f(x)]在[1，＋∞)上是单调减函数，求实数m的取值范围；

(2)设g(x)＝f(x)＋lnx，当m≥－2时，求g(x)在上的最大值．

设f(x)＝lo的奇函数，a为常数，

(Ⅰ)求a的值；

(Ⅱ)证明：f(x)在(1，＋∞)内单调递增；

(Ⅲ)若对于[3，4]上的每一个x的值，不等式f(x)＞()^x＋m恒成立，求实数m的取值范围．