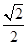题目内容
已知椭圆 的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若
的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若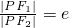 ,则e的值为
,则e的值为
- A.

- B.

- C.

- D.

B
分析:设P到椭圆左准线的距离为D,根据椭圆的第二定义可知|PF1|=ed,根据已知条件可知|PF2|=d,即椭圆和抛物线的准线重合,进而可以推断出椭圆的焦准距等于抛物线焦准距的一半,也等于椭圆自己的焦距,建立等式求得a和c的关系,进而求得离心率e.
解答:设P到椭圆左准线的距离为d,则|PF1|=ed
又因为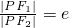 ?|PF1|=e|PF2|,所以|PF2|=d,
?|PF1|=e|PF2|,所以|PF2|=d,
即椭圆和抛物线的准线重合,而抛物线C2以F1为顶点,以F2为焦点
所以椭圆的焦准距等于抛物线焦准距的一半,也等于椭圆自己的焦距,即 -c=2c,
-c=2c,
解得a2=3c2,所以椭圆的离心率e= .
.
故选B
点评:本小题主要考查椭圆、双曲线的定义、椭圆的简单性质等基础知识,考查运算求解能力,考查数形结合思想.属于基础题.
分析:设P到椭圆左准线的距离为D,根据椭圆的第二定义可知|PF1|=ed,根据已知条件可知|PF2|=d,即椭圆和抛物线的准线重合,进而可以推断出椭圆的焦准距等于抛物线焦准距的一半,也等于椭圆自己的焦距,建立等式求得a和c的关系,进而求得离心率e.
解答:设P到椭圆左准线的距离为d,则|PF1|=ed
又因为
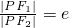 ?|PF1|=e|PF2|,所以|PF2|=d,
?|PF1|=e|PF2|,所以|PF2|=d,即椭圆和抛物线的准线重合,而抛物线C2以F1为顶点,以F2为焦点
所以椭圆的焦准距等于抛物线焦准距的一半,也等于椭圆自己的焦距,即
 -c=2c,
-c=2c,解得a2=3c2,所以椭圆的离心率e=
 .
.故选B
点评:本小题主要考查椭圆、双曲线的定义、椭圆的简单性质等基础知识,考查运算求解能力,考查数形结合思想.属于基础题.

练习册系列答案
相关题目
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
 如图,A,B是椭圆C:
如图,A,B是椭圆C:
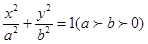 的离心率为e=
的离心率为e=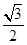 ,且过点(
,且过点(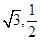 )
)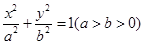 的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若
的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若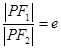 ,则e的值为( )
,则e的值为( )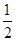 B.
B. 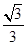 C.
C.
 D.
D.