题目内容
（本小题满分12分）
已知椭圆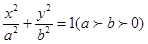
的离心率为e=
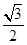，且过点（
）
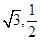（Ⅰ）求椭圆的方程；
（Ⅱ）设直线l：y=kx+m(k≠0，m＞0)与椭圆交于P，Q两点，且以PQ为对角线的菱形的一顶点为（-1，0），求：△OPQ面积的最大值及此时直线l的方程.
【答案】
.解：（Ⅰ）∵e=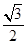
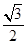∴c= a
∴b2=a2-c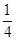2=
a2
故所求椭圆为：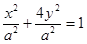
………………………………（1分）
又椭圆过点（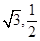
） ∴
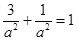∴a2 =4. b2 =1 ∴
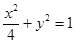（3分）
(Ⅱ)设P（x1,y1）, Q（x2,y2）,PQ的中点为（x0,y0）
将直线y=kx+m与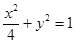
联立得（1+4k2）x2+8kmx+4m2-4=0
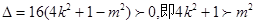①
又x0=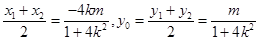
……………………（5分）
又点［-1，0）不在椭圆OE上，
依题意有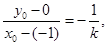
整理得3km=4k2+1 ②……………………………………………………（7分）
由①②可得k2＞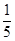
，∵m＞0,
∴k＞0,∴k＞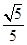
……………………（8分）
设O到直线l的距离为d，则
S△OPQ =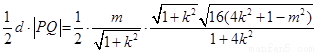
=
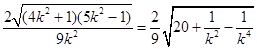……………………………（10分）
当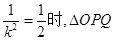
的面积取最大值1，此时k=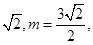
∴直线方程为y=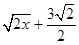
……………………………………（12分）
【解析】略
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
