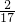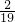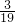Question

从混有5张假钞的20张百元钞票中任意抽取2张，将其中1张放在验钞机上检验发现是假钞，则另一张也是假钞的概率为（　　）

• A．

  2

  17

• B．

  4

  19

• C．

  2

  19

• D．

  3

  19

Answer 1

分析：设事件A表示“抽到的两张都是假钞”，事件B表示“抽到的两张至少有一张假钞”，所求的概率即 P（A/B）．
先求出P（AB）和P（B）的值，再根据P（A/B）=

P(AB)

P(B)

，运算求得结果．

解答：解：设事件A表示“抽到的两张都是假钞”，事件B表示“抽到的两张至少有一张假钞”，
则所求的概率即 P（A/B）．
又P（AB）=P（A）=

C 2 5

C 2 20

，P（B）=

C 2 5 +C 1 5 •C 1 15

C 2 20

，由公式P（A/B）=

P(AB)

P(B)

=

C 2 5

C 2 5 +C 1 5 •C 1 15

 
=

10

10+75

=

2

17

，
故选A．

点评：本题主要条件概率的求法，考查等可能事件的概率，体现了转化的数学思想．注意准确理解题意，看是在什么条件下
发生的事件，本题是求条件概率，而非古典概率，属于中档题．