题目内容
【题目】定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离,已知曲线C1:y=x2+a到直线l:y=x的距离等于曲线C2:x2+(y+4)2=2到直线l:y=x的距离,则实数a= .
【答案】![]()
【解析】解:圆x2+(y+4)2=2的圆心为(0,﹣4),半径为 ![]() ,
,
圆心到直线y=x的距离为 ![]() =2
=2 ![]() ,
,
∴曲线C2:x2+(y+4)2=2到直线l:y=x的距离为2 ![]() ﹣
﹣ ![]() =
= ![]() .
.
则曲线C1:y=x2+a到直线l:y=x的距离等于 ![]() ,
,
令y′=2x=1解得x= ![]() ,故切点为(
,故切点为( ![]() ,
, ![]() +a),
+a),
切线方程为y﹣( ![]() +a)=x﹣
+a)=x﹣ ![]() 即x﹣y﹣
即x﹣y﹣ ![]() +a=0,
+a=0,
由题意可知x﹣y﹣ ![]() +a=0与直线y=x的距离为
+a=0与直线y=x的距离为 ![]() ,
,
即 ![]() 解得a=
解得a= ![]() 或﹣
或﹣ ![]() .
.
当a=﹣ ![]() 时直线y=x与曲线C1:y=x2+a相交,故不符合题意,舍去.
时直线y=x与曲线C1:y=x2+a相交,故不符合题意,舍去.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解点到直线的距离公式的相关知识,掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: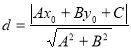 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目