Question

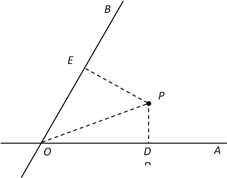
【题目】如图，有一直径为8米的半圆形空地，现计划种植甲、乙两种水果，已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍，但种植甲水果需要有辅助光照．半圆周上的处恰有一可旋转光源满足甲水果生长的需要，该光源照射范围是,点在直径上，且．

（1）若米，求的长；

（2）设, 求该空地产生最大经济价值时种植甲种水果的面积．

Answer 1

【答案】（1）1或3（2）

【解析】试题分析：（1）利用余弦定理即可求得；（2）设，由正弦定理求得,利用，计算面积，求出最大值，即可求该空地产生最大经济价值时种植甲种水果的面积．

试题解析：

解：（1）连结，已知点在以为直径的半圆周上，所以为直角三角形，

因为，，所以，，

在中由余弦定理，且，

所以，

解得或，

（2）因为，，

所以，

所以，

在中由正弦定理得：

所以，

在中，由正弦定理得：

所以，

若产生最大经济效益，则的面积最大，

，

因为，所以

所以当时，取最大值为，此时该地块产生的经济价值最大．