题目内容
已知椭圆C：
＋y2＝1(a>1)的上顶点为A，左、右焦点F1、F2，直线AF2与圆M：x2＋y2－6x－2y＋7＝0相切．
(1)求椭圆C的方程；
(2)若椭圆内存在动点P，使|PF1|，|PO|，|PF2|成等比数列(O为坐标原点)．求
的取值范围．
(2)由(1)知F1(－
，0)、F2(，0)，设P(x，y)，由题意知|PO|2＝|PF1|·|PF2|，
得x2－y2＝1，则x2＝y2＋1≥1.………………………………9分
因为点P在椭圆内，故
＋y2<1，即x2<
. ∴1≤x2<. ……………………12分
又＝x2－2＋y2＝2x2－3，
∴－1≤<0.…………………………14分
练习册系列答案
相关题目
＋y2＝1的两焦点为F1，F2，点P(x0，y0)满足0＜
＜1，则|PF1|＋|PF2|的取值范围为________，直线
＋y0y＝1与椭圆C的公共点个数为________．
＋y2＝1(a＞1)的上顶点为A，右焦点为F，直线AF与圆M：x2＋y2－6x－2y＋7＝0
相切．
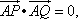求证：直线l过定点，并求出该定点N的坐标
＋y2＝1，过点(m,0)作圆x2＋y2＝1的切线l交椭圆G于A、B两点．
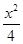＋y2＝1，过点(m,0)作圆x2＋y2＝1的切线l交椭圆G于A、B两点．