题目内容
如图,已知椭圆C:![]() +y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0
+y2=1(a>1)的上顶点为A,右焦点为F,直线AF与圆M:x2+y2-6x-2y+7=0![]() 相切.
相切.
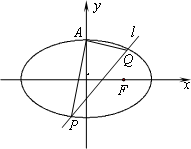
(Ⅰ)求椭圆C的方程;
(Ⅱ)若不过点A的动直线l与椭圆C相交于P、Q两点,且 求证:直线l过定点,并求出该定点N的坐标
求证:直线l过定点,并求出该定点N的坐标
答案:
解析:
解析:
|
(Ⅰ)将圆 由 即 由直线 当 故椭圆 (Ⅱ)(方法一)由 由 直线 将 并整理得: 解得 即 将上式中的 直线 化简得直线 因此直线 (方法二)由题直线 代入椭圆 设直线 由 整理得: 此时 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 如图,已知椭圆C:
如图,已知椭圆C: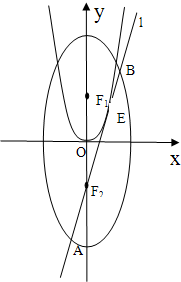 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆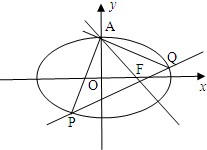 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C: