题目内容

函数f（x）=a|x-b|在区间[0，+∞）上是增函数，则实数a，b的取值范围是（　　）
A、a＞0，b≥0B、a＞0，b≤0C、a＜0，b≥0D、a＜0，b≤0
分析：由题意可得
a＞0
b≤0
，结合所给的选项，从而得出结论．
解答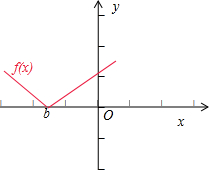：精英家教网解：由于函数f（x）=a|x-b|在区间[0，+∞）上是增函数，故有
a＞0
b≤0
，
如图所示：
故选 B．
点评：本题主要考查函数的单调性的性质，体现了数形结合的数学思想，属于基础题．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
定义在R上的奇函数f（x）满足f（2-x）=f（x），当x∈[0，1]时，f(x)=
x
．又g(x)=cos
πx
2
，则集合{x|f（x）=g（x）}等于（　　）
如果函数f（x）在x=x0处取得极值，则点（x0，f（x0））称为函数f（x）的一个极值点．已知函数f（x）=ax3+bx2+cx+d（a≠0，a，b，c，d∈R）的一个极值点恰为坐标系原点，且y=f（x）在x=1处的切线方程为3x+y-1=0．
（1）求函数f（x）的解析式；
（2）求函数f（x）在[-2，2]上的值域．
设函数f（x）是定义在R上的偶函数，且f（x+2）=f（x）恒成立；当x∈[0，1]时，f（x）=x3-4x+3．有下列命题：
①f(-
3
4
) ＜f(
15
2
)；
②当x∈[-1，0]时f（x）=x3+4x+3；
③f（x）（x≥0）的图象与x轴的交点的横坐标由小到大构成一个无穷等差数列；
④关于x的方程f（x）=|x|在x∈[-3，4]上有7个不同的根．
其中真命题的个数为（　　）
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网