题目内容
已知椭圆E的方程是 (a>b>0),其左顶点为(-2,0),离心率e=
(a>b>0),其左顶点为(-2,0),离心率e= .
.
(1)求椭圆E的方程;
(2)已知倾斜角为45°且过右焦点的直线l交椭圆E于A、B两点,若椭圆上存在一点P,使 =λ(
=λ( +
+ ),试求λ的值.
),试求λ的值.
解:(1)由已知得a=2,e= =
= ,∴c=1,b=
,∴c=1,b=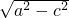 =
= ,
,
∴椭圆E的方程为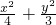 =1.
=1.
(2)由(1)得右焦点F(1,0),因此直线l的方程为y=x-1.
代入椭圆方程并整理得7x2-8x-8=0.
设A(x1,y1),B(x2,y2),则x1+x2= ,
,
∴y1+y2=(x1-1)+(x2-1)=(x1+x2)-2=- .
.
∴ =λ(
=λ( +
+ )=λ(x1+x2,y1+y2)=λ(
)=λ(x1+x2,y1+y2)=λ( ,-
,- ),
),
∴P点坐标为( ,-
,- ),
),
代入椭圆方程,可得 =1,
=1,
∴ ,解得λ=
,解得λ= .
.
分析:(1)利用椭圆左顶点为(-2,0),离心率e= ,结合b=
,结合b=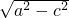 ,求出几何量,即可求椭圆E的方程;
,求出几何量,即可求椭圆E的方程;
(2)确定直线l的方程,代入椭圆方程并整理,利用韦达定理,结合 =λ(
=λ( +
+ ),求出P的坐标,代入椭圆方程,即可求λ的值.
),求出P的坐标,代入椭圆方程,即可求λ的值.
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.
 =
= ,∴c=1,b=
,∴c=1,b=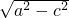 =
= ,
,∴椭圆E的方程为
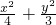 =1.
=1.(2)由(1)得右焦点F(1,0),因此直线l的方程为y=x-1.
代入椭圆方程并整理得7x2-8x-8=0.
设A(x1,y1),B(x2,y2),则x1+x2=
 ,
,∴y1+y2=(x1-1)+(x2-1)=(x1+x2)-2=-
 .
.∴
 =λ(
=λ( +
+ )=λ(x1+x2,y1+y2)=λ(
)=λ(x1+x2,y1+y2)=λ( ,-
,- ),
),∴P点坐标为(
 ,-
,- ),
),代入椭圆方程,可得
 =1,
=1,∴
 ,解得λ=
,解得λ= .
.分析:(1)利用椭圆左顶点为(-2,0),离心率e=
 ,结合b=
,结合b=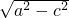 ,求出几何量,即可求椭圆E的方程;
,求出几何量,即可求椭圆E的方程;(2)确定直线l的方程,代入椭圆方程并整理,利用韦达定理,结合
 =λ(
=λ( +
+ ),求出P的坐标,代入椭圆方程,即可求λ的值.
),求出P的坐标,代入椭圆方程,即可求λ的值.点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
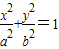 (a>b>0),其左顶点为(-2,0),离心率e=
(a>b>0),其左顶点为(-2,0),离心率e= .
.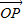 =λ(
=λ(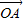 +
+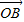 ),试求λ的值.
),试求λ的值.