题目内容
若函数f(x)＝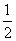
x2－x＋a的定义域和值域均为[1，b](b>1)，求a，b的值．
解 ∵f(x)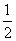＝(x－1)2＋a－，
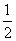∴其对称轴为x＝1，即函数f(x)在[1，b]上单调递增．
∴f(x)min＝f(1)＝a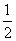－＝1，①
f(x)max＝f(b)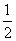＝b2－b＋a＝b，②
又b>1，由①②解得
∴a，b的值分别为
，3.
练习册系列答案
相关题目
题目内容
若函数f(x)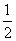＝x2－x＋a的定义域和值域均为[1，b](b>1)，求a，b的值．
解 ∵f(x)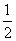＝(x－1)2＋a－，
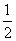∴其对称轴为x＝1，即函数f(x)在[1，b]上单调递增．
∴f(x)min＝f(1)＝a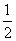－＝1，①
f(x)max＝f(b)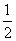＝b2－b＋a＝b，②
又b>1，由①②解得
∴a，b的值分别为，3.
且斜率为
的直线与圆
相交于
两点。求的
值
，则f
＋f
的定义域为( )
的值域为[－2,2]，则实数a的取值范围是( )
.
恒成立，求m的取值范围．