题目内容
对于椭圆x2+
解:设l的方程为y=kx+m,
由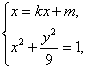 得(k2+9)x2+2kmx+m2-9=0,
得(k2+9)x2+2kmx+m2-9=0,
所以Δ=4k2m2-4(k2+9)(m2-9)>0,
即m2-k2-9<0.
又![]() ,
,
所以m=![]() .
.
所以![]() -(k2+9)<0.
-(k2+9)<0.
解得k2>3,即k>![]() 或k<-
或k<-![]() ,
,
所以倾斜角又满足![]() <α<
<α<![]() 或
或![]() <α<
<α<![]() ,即满足条件的直线l存在,其倾斜角的范围是(
,即满足条件的直线l存在,其倾斜角的范围是(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() ).
).

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
题目内容
对于椭圆x2+
解:设l的方程为y=kx+m,
由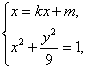 得(k2+9)x2+2kmx+m2-9=0,
得(k2+9)x2+2kmx+m2-9=0,
所以Δ=4k2m2-4(k2+9)(m2-9)>0,
即m2-k2-9<0.
又![]() ,
,
所以m=![]() .
.
所以![]() -(k2+9)<0.
-(k2+9)<0.
解得k2>3,即k>![]() 或k<-
或k<-![]() ,
,
所以倾斜角又满足![]() <α<
<α<![]() 或
或![]() <α<
<α<![]() ,即满足条件的直线l存在,其倾斜角的范围是(
,即满足条件的直线l存在,其倾斜角的范围是(![]() ,
,![]() )∪(
)∪(![]() ,
,![]() ).
).

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案