题目内容
已知椭圆C的对称中心为坐标原点O,焦点在x轴上,左右焦点分别为F1,F2,且|F1F2|=2| 5 |
| 5 |
| 4 |
| 3 |
(1)求椭圆C的方程;
(2)设椭圆C上的一点p在第一象限,且满足PF1⊥PF2,⊙O的方程为x2+y2=4.求点p坐标,并判断直线pF2与⊙O的位置关系;
(3)设点A为椭圆的左顶点,是否存在不同于点A的定点B,对于⊙O上任意一点M,都有
| MB |
| MA |
分析:(1)设出椭圆的标准方程,根据题意可求得焦点坐标,根据椭圆的定义和点(
,
)求得2a,进而根据a和c求得b,则椭圆的方程可得.
(2)设点P的坐标为(x,y),根据PF1⊥PF2,可得
•
=0,把x和y代入整理可得方程与椭圆方程联立求得x和y,即点P的坐标.进而可得直线PF2的方程,进而可求得⊙O圆心O到直线PF2的距离正好等于半径,进而推断直线PF2与⊙O相切.
(3)设点M的坐标为(x,y),假设存在点B(m,n),对于⊙O上任意一点M,都有
为常数,则可表示出|MB|2和|MA|2,代入
中,进而可得求得m,n和λ,求得点B的坐标.
| 5 |
| 4 |
| 3 |
(2)设点P的坐标为(x,y),根据PF1⊥PF2,可得
| PF1 |
| PF2 |
(3)设点M的坐标为(x,y),假设存在点B(m,n),对于⊙O上任意一点M,都有
| MB |
| MA |
| MB |
| MA |
解答:解:(1)设椭圆的方程为
+
=1,(a>b>0),由题意可得:
椭圆C两焦点坐标分别为F1(-
,0),F2(
,0)
由点(
,
)在该椭圆上,
∴2a=
+
=6.
∴a=3
又c=
得b2=9-5=4,
故椭圆的方程为
+
=1.
(2)设点P的坐标为(x,y)(x>0,y>0),则为
+
.①
由PF1⊥PF2,得
•
=0∴(x+
)(x-
)+y2=0
即x2+y2=5②
由①②联立结合x>0,y>0解得:x=
,y=
,即点P的坐标为(
,
)
∴直线PF2的方程为2x+y-2
=0
∵圆x2+y2=4的圆心O到直线PF2的距离d=
=2
∴直线PF2与⊙O相切
(3)设点M的坐标为(x,y),则x2+y2=4
假设存在点B(m,n),对于⊙O上任意一点M,都有
为常数,则
|MB|2=(x-m)2+(y-n)2,|MA|2=(x+3)2+y2
∴
=λ(常数)恒成立
可得(6λ+2m)x+2ny+13λ-m2-n2-4=0
∴
∴
或
(不合舍去)
∴存在满足条件的点B,它的坐标为(-
,0).
| x2 |
| a2 |
| y2 |
| b2 |
椭圆C两焦点坐标分别为F1(-
| 5 |
| 5 |
由点(
| 5 |
| 4 |
| 3 |
∴2a=
20+
|
0+
|
∴a=3
又c=
| 5 |
故椭圆的方程为
| x2 |
| 9 |
| y2 |
| 4 |
(2)设点P的坐标为(x,y)(x>0,y>0),则为
| x2 |
| 9 |
| y2 |
| 4 |
由PF1⊥PF2,得
| PF1 |
| PF2 |
| 5 |
| 5 |
即x2+y2=5②
由①②联立结合x>0,y>0解得:x=
3
| ||
| 5 |
4
| ||
| 5 |
3
| ||
| 5 |
4
| ||
| 5 |
∴直线PF2的方程为2x+y-2
| 5 |
∵圆x2+y2=4的圆心O到直线PF2的距离d=
2
| ||
|
∴直线PF2与⊙O相切
(3)设点M的坐标为(x,y),则x2+y2=4
假设存在点B(m,n),对于⊙O上任意一点M,都有
| MB |
| MA |
|MB|2=(x-m)2+(y-n)2,|MA|2=(x+3)2+y2
∴
| (x-m)2+(y-n) 2 |
| (x+3)2+y2 |
可得(6λ+2m)x+2ny+13λ-m2-n2-4=0
∴
|
∴
|
|
∴存在满足条件的点B,它的坐标为(-
| 4 |
| 3 |
点评:本题主要考查了椭圆的标准方程以及直线与椭圆与圆的关系.考查了学生综合分析问题和解决问题的能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
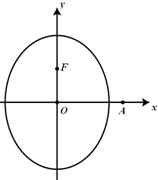 (2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=
(2013•泉州模拟)已知椭圆C的对称中心为坐标原点,上焦点为F(0,1),离心率e=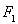
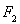
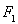
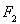
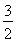
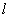

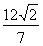
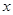 轴上,离心率为
轴上,离心率为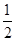 ,且点
,且点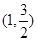 在该椭圆上。
在该椭圆上。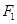 的直线
的直线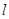 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若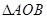 的面积为
的面积为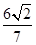 ,求圆心在原点O且与直线相切的圆的方程。
,求圆心在原点O且与直线相切的圆的方程。