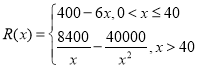题目内容
【题目】若函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() .
.
(1)求函数![]() 的解析式.
的解析式.
(2)若方程![]() 有
有![]() 个不同的根,求实数
个不同的根,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
先对函数求导,得到![]() ;
;
(1)根据题意,得到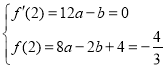 ,求解得出
,求解得出![]() ,即可得出结果;
,即可得出结果;
(2)先由导数的方法研究函数![]() 的单调性与极值,再将方程
的单调性与极值,再将方程![]() 有
有![]() 个不同的根,转化为直线
个不同的根,转化为直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点,结合函数图像,即可求出结果.
个交点,结合函数图像,即可求出结果.
因为![]() ,所以
,所以![]() .
.
(1)因为函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,
,
所以有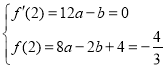 ,解得
,解得![]() ;
;
故所求函数的解析式为![]() ;
;
(2)由(1)可得![]() ,
,
令![]() ,得
,得![]() 或
或![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| + | 0 | - | 0 | + |
|
|
|
|
|
|
因此,当x=-2时,![]() 有极大值
有极大值![]() ,
,
当x=2时,![]() 有极小值
有极小值![]() ,
,
所以函数![]() 的图象大致如图所示.
的图象大致如图所示.
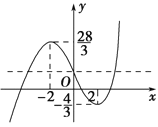
若![]() 有
有![]() 个不同的根,则直线
个不同的根,则直线![]() 与函数
与函数![]() 的图象有
的图象有![]() 个交点,
个交点,
所以![]() .
.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目