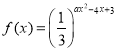题目内容
【题目】已知函数![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若直线![]() 与曲线
与曲线![]() 相切于点
相切于点![]() ,证明:
,证明:![]() ;
;
(Ⅱ)若不等式![]() 有且仅有两个整数解,求
有且仅有两个整数解,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析(2)![]()
【解析】
(Ⅰ)求得函数的导数![]() ,由导数的几何意义和直线
,由导数的几何意义和直线![]() 的图象过定点
的图象过定点![]() ,得到
,得到![]() ,设
,设![]() ,利用导数得到函数的单调性,根据零点的存在定理,即可求解.
,利用导数得到函数的单调性,根据零点的存在定理,即可求解.
(Ⅱ)由![]() 得
得![]() ,令
,令![]() ,利用导数和由(1)知
,利用导数和由(1)知![]() 在
在![]() 上单调递增,求得
上单调递增,求得![]() ,通过分类讨论
,通过分类讨论![]() 的范围,即可满足条件
的范围,即可满足条件![]() 的范围.
的范围.
(Ⅰ)![]() ,
,
由导数的几何意义可知,![]() , ①
, ①
又直线![]() 的图象过定点
的图象过定点![]() ,因此
,因此![]() ,
,
即![]() , ②
, ②
联立①②消去![]() 有
有![]() .
.
设![]() ,则
,则![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
而![]() ,
,![]() ,
,![]() ,
,
由函数零点存在性定理知![]() .
.
(Ⅱ)由![]() 得
得![]() ,
,
令![]() ,则
,则![]() ,
,
由(Ⅰ)知![]() 在
在![]() 上单调递增,
上单调递增,
且![]() 时,
时,![]() ;在
;在![]() ,
,![]() ,
,
故![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
∴![]() .
.
易证![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
(1)若![]() ,则
,则![]() ,
,
此时![]() 有无穷多个整数解,不合题意;
有无穷多个整数解,不合题意;
(2)若![]() ,即
,即![]() ,因为
,因为![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() ,
,![]() ,
,
所以![]() 无整数解,不合题意;
无整数解,不合题意;
(3)若![]() ,即
,即![]() ,此时
,此时![]() ,故0,1是
,故0,1是![]() 的两个整数解,又
的两个整数解,又![]() 只有两个整数解,因此
只有两个整数解,因此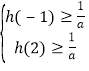 ,
,
解得![]() ,所以
,所以![]() .
.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目