题目内容
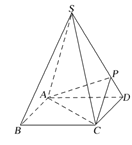
【题目】已知四棱锥![]() 的底面
的底面![]() 是菱形.
是菱形.
(1)若![]() ,求证:
,求证:![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,若
上的点,若![]() 平面
平面![]() ,
,![]() ,求
,求![]() 的值;
的值;
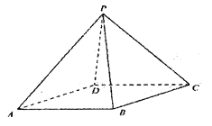
(3)若![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,判断
,判断![]() 是否为等腰三角形?并说明理由.
是否为等腰三角形?并说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 不可能为等腰三角形,理由见解析.
不可能为等腰三角形,理由见解析.
【解析】
(1)作辅助线,利用线面垂直的判定定理证明即可;
(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,利用平行的传递性以及线面平行的性质得出四边形
,利用平行的传递性以及线面平行的性质得出四边形![]() 为平行四边形,进而得出
为平行四边形,进而得出![]() ,结合相似三角形的性质得出
,结合相似三角形的性质得出![]() 的值;
的值;
(3)作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,由面面垂直,线面垂直的性质定理得出
,由面面垂直,线面垂直的性质定理得出![]() ,根据直角三角形斜边大于直角边,钝角三角形钝角所对的边大于另外两边,得出
,根据直角三角形斜边大于直角边,钝角三角形钝角所对的边大于另外两边,得出![]() ,
,![]() ,由等腰三角形的性质得出
,由等腰三角形的性质得出![]() ,进而得到
,进而得到![]() ,即可得出
,即可得出![]() 不可能为等腰三角形.
不可能为等腰三角形.
(1)证明:设![]() ,连接
,连接![]()
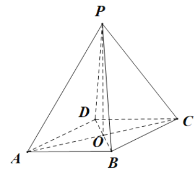
因为四边形![]() 是菱形,所以
是菱形,所以![]() ,
,![]() .
.
因为![]() ,所以
,所以![]() .
.
因为![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,
,
在菱形![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() ,所以
,所以![]() ,
,![]() ,
,![]() ,
,![]() 共面.
共面.
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
所以![]() .
.
所以四边形![]() 为平行四边形.所以
为平行四边形.所以![]() .
.
因为![]() ,所以
,所以![]() .
.
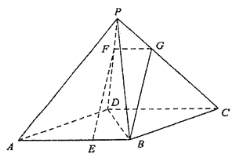
(3)![]() 不可能为等腰三角形,理由如下:
不可能为等腰三角形,理由如下:
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]()
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
所以![]() .
.
因为![]() ,
,![]() ,
,![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
所以![]() ,且
,且![]() .
.
所以![]() .所以
.所以![]() .
.
在菱形![]() 中,若
中,若![]() ,所以
,所以![]() 是等边三角形.
是等边三角形.
所以![]() 为
为![]() 的中点,所以
的中点,所以![]() ,
,
∴![]()
![]()
![]()
即![]() .
.
所以![]() 不可能为等腰三角形.
不可能为等腰三角形.


练习册系列答案
相关题目