题目内容
(本小题满分13分)如图,三棱柱 中,
中, ,
, ,
, .
.

(1)证明: ;
;
(2)若 ,
, ,求三棱锥
,求三棱锥 的体积.
的体积.
(1)证明详见解析;(2)1.
【解析】
试题分析:本题主要考查线线垂直、线面垂直、三棱锥的体积等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、计算能力.第一问,在等腰三角形中,O为AB中点,所以CO为高,由已知可得 为等边三角形,所以得到
为等边三角形,所以得到 ,所以利用线面垂直的判定得
,所以利用线面垂直的判定得 平面
平面 ,最后利用线面垂直的性质得
,最后利用线面垂直的性质得 ;第二问,在等边
;第二问,在等边 和
和 中,先解出CO和
中,先解出CO和 的长,判断得出
的长,判断得出 是直角三角形,所以得证
是直角三角形,所以得证 平面
平面 ,再利用三棱锥的体积公式计算即可.
,再利用三棱锥的体积公式计算即可.
试题解析:(1)证明:取 的中点
的中点 ,连接
,连接 ,
, ,
, .
.
 ,故
,故 , 2分
, 2分
又 ,
, .
.
 为等边三角形.
为等边三角形.
 , 4分
, 4分
又因为 平面
平面 ,
, 平面
平面 ,
, .
.
 平面
平面 . 6分
. 6分
又 平面
平面 ,因此
,因此 ; 7分
; 7分
(2)【解析】
在等边 中
中 ,在等边
,在等边 中
中 ;
;
在 中
中 .
.

 是直角三角形,且
是直角三角形,且 ,故
,故 . 9分
. 9分
又 、
、 平面
平面 ,
, ,
,
 平面
平面 .
.
故 是三棱锥
是三棱锥 的高. 10分
的高. 10分
又 .
.
 三棱锥
三棱锥 的体积
的体积 .
.
 三棱锥
三棱锥 的体积为1. 13分
的体积为1. 13分
考点:线线垂直、线面垂直、三棱锥的体积.

练习册系列答案
相关题目
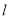 ,过A作直线
,过A作直线 的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为 .
的垂线AD,D为垂足,AD与圆O交于点E,则线段AE的长为 .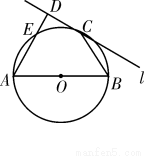

 与双曲线
与双曲线
 的焦点重合,且双曲线
的焦点重合,且双曲线 的渐近线为
的渐近线为 ,则双曲线
,则双曲线 的实轴长为( )
的实轴长为( ) B.
B. C.
C. D.
D.
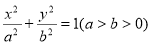 ,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若四边形PAOB为正方形,则椭圆的离心率为( )
,以O为圆心,短半轴长为半径作圆O,过椭圆的长轴的一端点P作圆O的两条切线,切点为A、B,若四边形PAOB为正方形,则椭圆的离心率为( )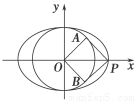
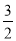 B.
B.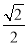 C.
C.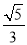 D.
D.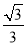
 和直线
和直线 平行,则a=( )
平行,则a=( ) B.
B. C.7或1 D.
C.7或1 D.
 ,
, ,在线段
,在线段 上任投一点
上任投一点 ,则
,则 的概率为 .
的概率为 .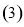 班共有学生
班共有学生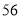 人,现根据座号,用系统抽样的方法,抽取一个容量为
人,现根据座号,用系统抽样的方法,抽取一个容量为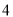 的样本.已知
的样本.已知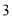 号、
号、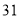 号、
号、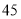 号同学在样本中,那么样本中还有一个同学的座号是( )
号同学在样本中,那么样本中还有一个同学的座号是( )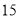 B.
B.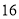 C.
C.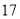 D.
D.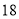
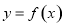 (
(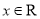 )满足
)满足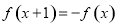 ,且
,且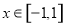 时,
时,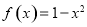 ,已知函数
,已知函数 ,则函数
,则函数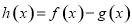 在区间
在区间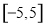 内的零点的个数为( )
内的零点的个数为( )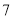 B.
B.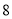 C.
C.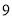 D.
D.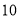
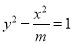 的离心率
的离心率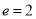 ,则以双曲线的两条渐近线与抛物线
,则以双曲线的两条渐近线与抛物线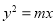 的交点为顶点的三角形的面积为
的交点为顶点的三角形的面积为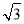 B.
B. C.
C.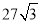 D.
D.