题目内容
14.设f(x)=x2+|x-a|.(1)当a=0时,试作出f(x)的图象,并写出函数f(x)的单调区间;
(2)求f(x)的最小值.
分析 (1)当a=0时,f(x)=x2+|x|=$\left\{\begin{array}{l}{x}^{2}-x,x<0\\{x}^{2}+x,x≥0\end{array}\right.$,结合二次函数的图象和性质,分段画出函数的图象,进而分析出函数的单调区间;
(2)f(x)=x2+|x-a|=$\left\{\begin{array}{l}{x}^{2}-x+a,x<a\\{x}^{2}+x-a,x≥a\end{array}\right.$,结合二次函数的图象和性质,分类讨论各种情况下f(x)的最小值,可得答案.
解答 解:(1)当a=0时,f(x)=x2+|x|=$\left\{\begin{array}{l}{x}^{2}-x,x<0\\{x}^{2}+x,x≥0\end{array}\right.$.
f(x)的图象如下图所示: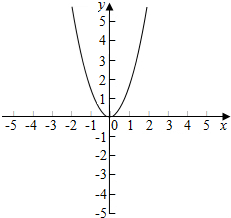
由图可得:函数f(x)的单调递增区间为:[0,+∞),单调递减区间为(-∞,0];
(2)f(x)=x2+|x-a|=$\left\{\begin{array}{l}{x}^{2}-x+a,x<a\\{x}^{2}+x-a,x≥a\end{array}\right.$,
当a≤$-\frac{1}{2}$时,函数f(x)的单调递增区间为:[$-\frac{1}{2}$,+∞),单调递减区间为(-∞,-$\frac{1}{2}$],当x=-$\frac{1}{2}$时,f(x)的最小值为:$-\frac{1}{4}$-a;
当$-\frac{1}{2}$<a<$\frac{1}{2}$时,函数f(x)的单调递增区间为:[a,+∞),单调递减区间为(-∞,a],当x=a时,f(x)的最小值为:a2;
当a≥$\frac{1}{2}$时,函数f(x)的单调递增区间为:[,+∞),单调递减区间为(-∞,$\frac{1}{2}$],当x=$\frac{1}{2}$时,f(x)的最小值为:a$-\frac{1}{4}$;
点评 本题考查的知识点是二次函数的图象和性质,熟练掌握二次函数的图象和性质是解答的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-∞,$\frac{1}{2}$) | B. | (-∞,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) | ||
| C. | (-∞,-$\frac{2}{3}$)∪(-$\frac{2}{3}$,+∞) | D. | (-∞,-$\frac{2}{3}$)∪(-$\frac{2}{3}$,$\frac{1}{2}$)∪($\frac{1}{2}$,+∞) |
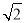 的像和B中元素-1的原像.
的像和B中元素-1的原像.