题目内容
(本小题14分)已知数列{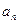 }的前
}的前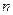 项和为
项和为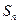 ,且
,且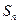 =
=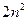 (
(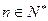 );
);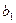 =3
=3
且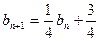 (
(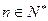 ),
),
(1)写出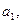
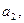
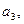
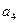 ;
;
(2)求数列{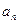 },{
},{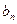 }的通项公式
}的通项公式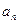 和
和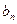 ;
;
(3)设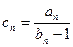 ,求数列
,求数列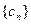 的前
的前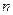 项和
项和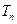 .
.
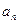 }的前
}的前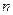 项和为
项和为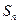 ,且
,且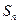 =
=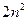 (
(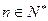 );
);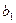 =3
=3且
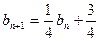 (
(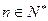 ),
),(1)写出
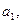
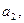
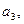
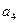 ;
;(2)求数列{
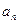 },{
},{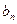 }的通项公式
}的通项公式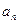 和
和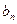 ;
;(3)设
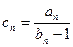 ,求数列
,求数列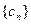 的前
的前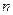 项和
项和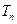 .
.解:(1)


 ……………………………(4分)
……………………………(4分)
(2) 由题意 =
=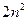 ,当n≥2时
,当n≥2时 ,
,
两式相减得
 ,
,
当n=1时, =2也满足,∴
=2也满足,∴
 (
(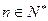 );
);
由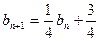 ,知
,知 即
即
∴数列{ }是以首项为2,公比为
}是以首项为2,公比为 的等比数列,
的等比数列,
∴ =
= ,
,
∴
 +1(
+1(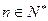 ). (9分)
). (9分)
(2)∵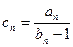 =
= =
= ,
,

两式相减得
 (14分)
(14分)



 ……………………………(4分)
……………………………(4分)(2) 由题意
 =
=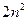 ,当n≥2时
,当n≥2时 ,
,两式相减得

 ,
,当n=1时,
 =2也满足,∴
=2也满足,∴
 (
(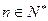 );
);由
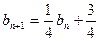 ,知
,知 即
即
∴数列{
 }是以首项为2,公比为
}是以首项为2,公比为 的等比数列,
的等比数列,∴
 =
= ,
,∴

 +1(
+1(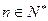 ). (9分)
). (9分)(2)∵
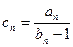 =
= =
= ,
,
两式相减得
 (14分)
(14分)略

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
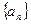 的通项公式为
的通项公式为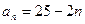 ,求数列
,求数列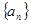 中,各项都是正数,且
中,各项都是正数,且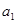 ,
,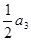 ,
,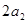 成等差数列,则
成等差数列,则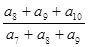 的值为
的值为


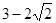
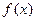 的图象经过点
的图象经过点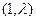 ,且对任意
,且对任意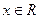 ,都有
,都有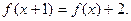 数列
数列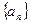 满足
满足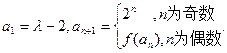
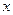 为正整数时,求
为正整数时,求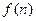 的表达式
的表达式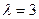 ,求
,求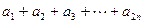
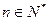 ,总有
,总有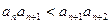 ,求实数
,求实数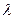 的取值范围
的取值范围 的前
的前 项和
项和 ,在数列
,在数列 中,
中, ,
,
 ,求数列
,求数列 前
前 。
。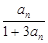 ,a1=2,则a4为 ( )
,a1=2,则a4为 ( )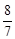
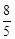
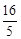
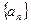
 满足前2项的和为5,前6项的和为3.
满足前2项的和为5,前6项的和为3.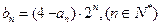 ,求数列
,求数列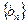 的前
的前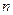 项和
项和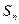
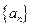 中,
中,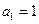 ,前
,前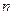 项和
项和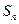 满足条件
满足条件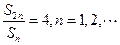 ,
,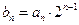 ,求数列
,求数列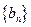 的前
的前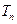 .
. 满足
满足 ,
, ,则该数列的通项公式
,则该数列的通项公式 .
.